题目内容
15、类比平面几何中的定理:△ABC中,若DE是△ABC的中位线,则有S△ADE:S△ABC=1:4;若三棱锥A-BCD有中截面EFG∥平面BCD,则截得三棱锥的体积与原三棱锥体积之间的关系式为
VA-EFG:VA-BCD=1:8
.分析:这是一个类比推理的题,在由平面图形到空间图形的类比推理中,一般是由点的性质类比推理到线的性质,由线的性质类比推理到面的性质,由面积的性质类比推理到体积的性质,由已知“若DE是△ABC的中位线,则有S△ADE:S△ABC=1:4”我们可以类比这一性质,推理出若三棱锥A-BCD中,有中截面EFG∥平面BCD,则截得三棱锥的体积与原三棱锥体积之间的关系式.
解答:解:由:△ABC中,若DE是△ABC的中位线,则有S△ADE:S△ABC=1:4;
我们可以根据由面积的性质类比推理到体积的性质,类比这一性质,推理出:
若三棱锥A-BCD有中截面EFG∥平面BCD,则截得三棱锥的体积与原三棱锥体积之间的关系式为
VA-EFG:VA-BCD=1:8
故答案为:VA-EFG:VA-BCD=1:8.
我们可以根据由面积的性质类比推理到体积的性质,类比这一性质,推理出:
若三棱锥A-BCD有中截面EFG∥平面BCD,则截得三棱锥的体积与原三棱锥体积之间的关系式为
VA-EFG:VA-BCD=1:8
故答案为:VA-EFG:VA-BCD=1:8.
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 是三条直线,若
是三条直线,若 ,则
,则 ∥
∥ ”,得出如下结论:
”,得出如下结论: 是两条直线,
是两条直线,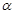 是平面,若
是平面,若 ,则
,则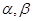 是两个平面,
是两个平面,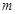 是直线,若
是直线,若 则
则 ;
;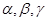 是三个平面,若
是三个平面,若 ,则
,则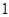 B.
B.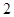 C.
C.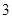 D.
D.