题目内容
【题目】直线l1 , l2分别是函数f(x)=sinx,x∈[0,π]图象上点P1 , P2处的切线,l1 , l2垂直相交于点P,且l1 , l2分别与y轴相交于点A,B,则△PAB的面积为
【答案】![]()
【解析】解:函数f(x)=sinx的导数为f′(x)=cosx,
设P1(x1,sinx1),P2(x2,sinx2),(设x1<x2),
可得图象上点P1,P2处的切线斜率为cosx1,cosx2,
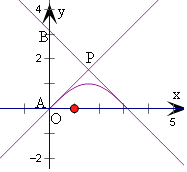
由l1,l2垂直,可得cosx1cosx2=﹣1,
由余弦函数的值域,可得cosx1=1,cosx2=﹣1,
即有x1=0,x2=π,
可得切线l1的方程为y=x,
l2的方程为y﹣0=﹣(x﹣π),即y=﹣x+π,
解得P( ![]() ,
, ![]() ),
),
由A(0,0),B(0,π),
可得△PAB的面积为 ![]() ×π×
×π× ![]() =
= ![]() .
.
所以答案是: ![]() .
.

练习册系列答案
相关题目
【题目】为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了1000名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合计 | |
男大学生 | 610 | ||
女大学生 | 90 | ||
合计 | 800 |
(1)根据题意完成表格;
(2)是否有95%的把握认为愿意做志愿者工作与性别有关? 参考公式及数据: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥K0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
K0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |

