题目内容
【题目】已知函数y=f(x)的定义在实数集R上的奇函数,且当x∈(﹣∞,0)时,xf′(x)<f(﹣x)(其中f′(x)是f(x)的导函数),若a= ![]() f(
f( ![]() ),b=(lg3)f(lg3),c=(log2
),b=(lg3)f(lg3),c=(log2 ![]() )f(log2
)f(log2 ![]() ),则( )
),则( )
A.c>a>b
B.c>b>a
C.a>b>c
D.a>c>b
【答案】A
【解析】解:设F(x)=xf(x),得F'(x)=x'f(x)+xf'(x)=xf'(x)+f(x),
∵当x∈(﹣∞,0)时,xf′(x)<f(﹣x),且f(﹣x)=﹣f(x)
∴当x∈(﹣∞,0)时,xf′(x)+f(x)<0,即F'(x)<0
由此可得F(x)=xf(x)在区间(﹣∞,0)上是减函数,
∵函数y=f(x)是定义在实数集R上的奇函数,
∴F(x)=xf(x)是定义在实数集R上的偶函数,在区间(0,+∞)上F(x)=xf(x)是增函数.
∵0<lg3<lg10=1, ![]() ∈(1,2)
∈(1,2)
∴F(2)>F( ![]() )>F(lg3)
)>F(lg3)
∵ ![]() =﹣2,从而F(
=﹣2,从而F( ![]() )=F(﹣2)=F(2)
)=F(﹣2)=F(2)
∴F( ![]() )>F(
)>F( ![]() )>F(lg3)
)>F(lg3)
即 ![]() >
> ![]() >(lg3)f(lg3),得c>a>b
>(lg3)f(lg3),得c>a>b
所以答案是:A
【考点精析】本题主要考查了对数值大小的比较和导数的几何意义的相关知识点,需要掌握几个重要的对数恒等式:![]() ,
,![]() ,
,![]() ;常用对数:
;常用对数:![]() ,即
,即![]() ;自然对数:
;自然对数:![]() ,即
,即![]() (其中
(其中![]() …);通过图像,我们可以看出当点
…);通过图像,我们可以看出当点![]() 趋近于
趋近于![]() 时,直线
时,直线![]() 与曲线相切.容易知道,割线
与曲线相切.容易知道,割线![]() 的斜率是
的斜率是![]() ,当点
,当点![]() 趋近于
趋近于![]() 时,函数
时,函数![]() 在
在![]() 处的导数就是切线PT的斜率k,即
处的导数就是切线PT的斜率k,即![]() 才能正确解答此题.
才能正确解答此题.

【题目】如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用![]() (单位:万元)和利润
(单位:万元)和利润![]() (单位:十万元)之间的关系,得到下列数据:
(单位:十万元)之间的关系,得到下列数据:
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
请回答:
(Ⅰ)请用相关系数![]() 说明
说明![]() 与
与![]() 之间是否存在线性相关关系(当
之间是否存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(Ⅱ)根据1的判断结果,建立![]() 与
与![]() 之间的回归方程,并预测当
之间的回归方程,并预测当![]() 时,对应的利润
时,对应的利润![]() 为多少(
为多少(![]() 精确到
精确到![]() ).
).
附参考公式:回归方程中![]() 中
中![]() 和
和![]() 最小二乘估计分别为
最小二乘估计分别为 ,
,![]() ,
,
相关系数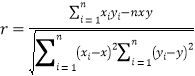 .
.
参考数据: ![]() .
.