题目内容

函数y=|tan(2x-
π
3
)|的周期为
π
2
π
2
．
分析：先求出函数y=tan（2x-
π
3
）的周期为
π
2
，结合函数的图象特征可得函数y=|tan(2x-
π
3
)|的周期．
解答：解：由于函数y=tan（2x-
π
3
）的周期为
π
2
，结合函数的图象特征可得，函数y=|tan(2x-
π
3
)|的图象，
是把函数y=tan（2x-
π
3
）的图象中位于x轴下方的部分沿着x轴对称到x轴的上方去，位于x轴上方的部分保持不变得到的，
故函数y=|tan(2x-
π
3
)|的不变，周期仍为
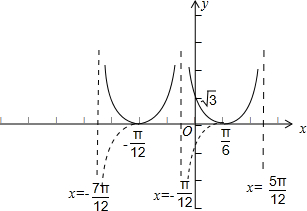
π
2
，
故答案为
π
2
．
函数y=|tan(2x-
π
3
)| 的图象如图所示：
点评：本题主要考查正切函数的图象特征，正切函数的周期性，属于中档题．
练习册系列答案
相关题目
函数y=tan（2x+
π
6
）的周期是（　　）
函数y=tan(
π
4
x-
π
2
)（0＜x＜4）的图象如图所示，A为图象与x轴的交点，过点A的直线l与函数的图象交于B、C两点，则(
OB
+
OC
)•
OA
=
8
8
．
函数y=tan（2x-
π
4
）的单调增区间是（　　）
在下列结论中：
①函数y=sin（kπ-x）（k∈Z）为奇函数；
②函数y=tan(2x+
π
6
)的图象关于点(
π
12
，0)对称；
③函数y=cos(2x+
π
3
)的图象的一条对称轴为x=-
2
3
π；
④若tan（π-x）=2，则cos2x=
1
5
．
其中正确结论的序号为
①③④
①③④
（把所有正确结论的序号都填上）．
若函数y=f（x）存在反函数y=f-1（x），且函数y=tan
πx
6
-f(x)的图象过点(2，
3
-
1
3
)，则函数y=f-1（x）-（arcsinx+arccosx）的图象一定过点
(
1
3
，2-
π
2
)
(
1
3
，2-
π
2
)
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网