题目内容
如图,AB是底部B不可到达的一个塔型建筑物,A为塔的最高点.现需在对岸测出塔高AB,甲、乙两同学各提出了一种测量方法,甲同学的方法是:选与塔底B在同一水平面内的一条基线CD,使C,D,B三点不在同一条直线上,测出∠DCB及∠CDB的大小(分别用α,β表示测得的数据)以及C,D间的距离(用s表示测得的数据),另外需在点C测得塔顶A的仰角(用θ表示测量的数据),就可以求得塔离AB.乙同学的方法是:选一条水平基线EF,使E,F,B三点在同一条直线上.在E,F处分别测得塔顶A的仰角(分别用α,β表示测得的数据)以及E,F间的距离(用s表示测得的数据),就可以求得塔高AB.请从甲或乙的想法中选出一种测量方法,写出你的选择并按如下要求完成测量计算:
①画出测量示意图;
②用所叙述的相应字母表示测量数据,画图时C,D,B按顺时针方向标注,E,F按从左到右的方向标注;
③求塔高AB.

【答案】分析:分别按照甲、乙的想法,构造三角形,利用正弦定理,即可求解.
解答: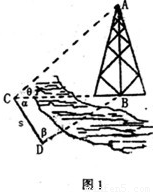 解:选甲,如图1,在△BCD中,∠CBD=π-α-β,由正弦定理可得
解:选甲,如图1,在△BCD中,∠CBD=π-α-β,由正弦定理可得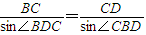
∴BC=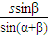
在直角△ABC中,AB=BCtan∠ACB=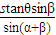 ;
;
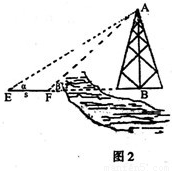
选乙,如图2,
在△AEF中,∠EAF=β-α,由正弦定理可得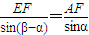
∴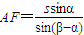
在直角△ABF中,AB=AFsinβ=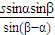 .
.
点评:本题考查正弦定理的运用,解题的关键是正确选择三角形,属于中档题.
解答:
 解:选甲,如图1,在△BCD中,∠CBD=π-α-β,由正弦定理可得
解:选甲,如图1,在△BCD中,∠CBD=π-α-β,由正弦定理可得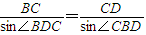
∴BC=
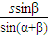
在直角△ABC中,AB=BCtan∠ACB=
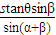 ;
;选乙,如图2,
在△AEF中,∠EAF=β-α,由正弦定理可得
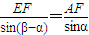
∴
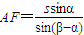
在直角△ABF中,AB=AFsinβ=
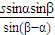 .
.
点评:本题考查正弦定理的运用,解题的关键是正确选择三角形,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
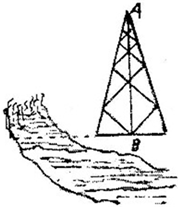 (2012•包头一模)如图,AB是底部B不可到达的一个塔型建筑物,A为塔的最高点.现需在对岸测出塔高AB,甲、乙两同学各提出了一种测量方法,甲同学的方法是:选与塔底B在同一水平面内的一条基线CD,使C,D,B三点不在同一条直线上,测出∠DCB及∠CDB的大小(分别用α,β表示测得的数据)以及C,D间的距离(用s表示测得的数据),另外需在点C测得塔顶A的仰角(用θ表示测量的数据),就可以求得塔离AB.乙同学的方法是:选一条水平基线EF,使E,F,B三点在同一条直线上.在E,F处分别测得塔顶A的仰角(分别用α,β表示测得的数据)以及E,F间的距离(用s表示测得的数据),就可以求得塔高AB.
(2012•包头一模)如图,AB是底部B不可到达的一个塔型建筑物,A为塔的最高点.现需在对岸测出塔高AB,甲、乙两同学各提出了一种测量方法,甲同学的方法是:选与塔底B在同一水平面内的一条基线CD,使C,D,B三点不在同一条直线上,测出∠DCB及∠CDB的大小(分别用α,β表示测得的数据)以及C,D间的距离(用s表示测得的数据),另外需在点C测得塔顶A的仰角(用θ表示测量的数据),就可以求得塔离AB.乙同学的方法是:选一条水平基线EF,使E,F,B三点在同一条直线上.在E,F处分别测得塔顶A的仰角(分别用α,β表示测得的数据)以及E,F间的距离(用s表示测得的数据),就可以求得塔高AB. 如图,AB是底部B不可到达的一个塔型建筑物,A为塔的最高点.现需在对岸测出塔高AB,甲、乙两同学各提出了一种测量方法,甲同学的方法是:选与塔底B在同一水平面内的一条基线CD,使C,D,B三点不在同一条直线上,测出∠DCB及∠CDB的大小(分别用α,β表示测得的数据)以及C,D间的距离(用s表示测得的数据),另外需在点C测得塔顶A的仰角(用θ表示测量的数据),就可以求得塔离AB.乙同学的方法是:选一条水平基线EF,使E,F,B三点在同一条直线上.在E,F处分别测得塔顶A的仰角(分别用α,β表示测得的数据)以及E,F间的距离(用s表示测得的数据),就可以求得塔高AB.
如图,AB是底部B不可到达的一个塔型建筑物,A为塔的最高点.现需在对岸测出塔高AB,甲、乙两同学各提出了一种测量方法,甲同学的方法是:选与塔底B在同一水平面内的一条基线CD,使C,D,B三点不在同一条直线上,测出∠DCB及∠CDB的大小(分别用α,β表示测得的数据)以及C,D间的距离(用s表示测得的数据),另外需在点C测得塔顶A的仰角(用θ表示测量的数据),就可以求得塔离AB.乙同学的方法是:选一条水平基线EF,使E,F,B三点在同一条直线上.在E,F处分别测得塔顶A的仰角(分别用α,β表示测得的数据)以及E,F间的距离(用s表示测得的数据),就可以求得塔高AB.
