题目内容
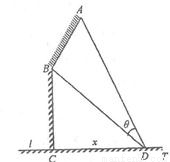
 如图,在海岸线l一侧C处有一个美丽的小岛,某旅游公司为方便游客,在l上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米.公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛.据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠CDA=α,每批游客从各自报名点到C岛所需运输成本S元.
如图,在海岸线l一侧C处有一个美丽的小岛,某旅游公司为方便游客,在l上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米.公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛.据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠CDA=α,每批游客从各自报名点到C岛所需运输成本S元.
(1)写出S关于α的函数表达式,并指出α的取值范围;
(2)问中转点D距离A处多远时,S最小?
解:(1)由题在△ACD中, .
.
由正弦定理知 ,得
,得 …(3分)∴
…(3分)∴ =
= …(7分)
…(7分)
(2)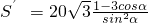 ,令S′=0,得
,令S′=0,得 …(10分)
…(10分)
当 时,S′<0;当
时,S′<0;当 时,S′>0,∴当
时,S′>0,∴当 时S取得最小值…(12分)
时S取得最小值…(12分)
此时 ,
,
∴中转站距A处 千米时,运输成本S最小…(14分)
千米时,运输成本S最小…(14分)
分析:(1)由题在△ACD中,由余弦定理求得CD、AD的值,即可求得运输成本S的解析式.
(2)利用导数求得cosα= 时,函数S取得极小值,由此可得中转点D到A的距离以及S的最小值.
时,函数S取得极小值,由此可得中转点D到A的距离以及S的最小值.
点评:本题主要考查正弦定理,利用导数研究函数的单调性,由函数的单调性求极值,属于中档题.
 .
.由正弦定理知
 ,得
,得 …(3分)∴
…(3分)∴ =
= …(7分)
…(7分)(2)
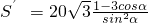 ,令S′=0,得
,令S′=0,得 …(10分)
…(10分)当
 时,S′<0;当
时,S′<0;当 时,S′>0,∴当
时,S′>0,∴当 时S取得最小值…(12分)
时S取得最小值…(12分)此时
 ,
,∴中转站距A处
 千米时,运输成本S最小…(14分)
千米时,运输成本S最小…(14分)分析:(1)由题在△ACD中,由余弦定理求得CD、AD的值,即可求得运输成本S的解析式.
(2)利用导数求得cosα=
 时,函数S取得极小值,由此可得中转点D到A的距离以及S的最小值.
时,函数S取得极小值,由此可得中转点D到A的距离以及S的最小值.点评:本题主要考查正弦定理,利用导数研究函数的单调性,由函数的单调性求极值,属于中档题.

练习册系列答案
相关题目
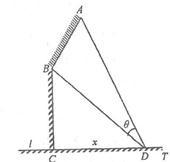 如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60°(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60°(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4 (2013•盐城二模)如图,在海岸线l一侧C处有一个美丽的小岛,某旅游公司为方便游客,在l上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米.公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛.据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠CDA=α,每批游客从各自报名点到C岛所需运输成本S元.
(2013•盐城二模)如图,在海岸线l一侧C处有一个美丽的小岛,某旅游公司为方便游客,在l上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米.公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛.据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠CDA=α,每批游客从各自报名点到C岛所需运输成本S元.
 . D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为θ.
. D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为θ.