题目内容
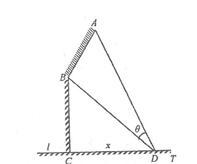
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60度(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离 . D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为θ.
. D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为θ.(Ⅰ)将tanθ表示为x的函数;
(Ⅱ)求点D的位置,使θ取得最大值.
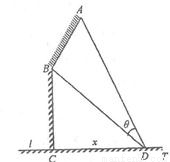
【答案】分析:(Ⅰ)过A分别作直线CD,BC的垂线,求出AE,在直角三角形中,设CD=x,利用三角函数tan∠BCD,讨论x的取值范围得到tan∠ADC有两种情况求得结果一样,而tanθ等于tan∠ADC-tan∠BDC,利用正切公式tan(α-β)= 求出其值即可.
求出其值即可.
(Ⅱ)根据 当且仅当a=b时取等号的方法,求出tanθ的最大值,根据正切函数是单调增函数得到x的值表示出D的位置即可.
当且仅当a=b时取等号的方法,求出tanθ的最大值,根据正切函数是单调增函数得到x的值表示出D的位置即可.
解答:解:(Ⅰ)过A分别作直线CD,BC的垂线,垂足分别为E,F.由题可知,AB=4.5,BC=4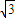 ,∠ABF=90°-60°=30°,
,∠ABF=90°-60°=30°,
所以CE=AF=4.5×sin30°= ,BF=4.5×cos30°=
,BF=4.5×cos30°=
 ,AE=CF=BC+BF=
,AE=CF=BC+BF=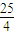
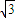 .
.
因为CD=x(x>0).所以tan∠BDC=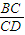 =
=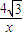 .
.
当x> 时,ED=x-
时,ED=x- ,tan∠ADC=
,tan∠ADC=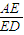 =
=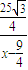 =
=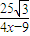 (如图1).
(如图1).
当0<x< 时,ED=
时,ED= -x,tan∠ADC=
-x,tan∠ADC=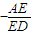 =
=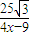 (如图2).
(如图2).
所以tanθ=tan∠ADB=tan(∠ADC-∠BDC)=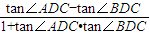 =
= =
= ,其中x>0且x≠
,其中x>0且x≠ .
.
当x= 时,tanθ=
时,tanθ= =
=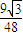 ,符合上式.
,符合上式.
所以tanθ=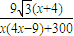 .x>0
.x>0
图1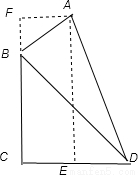 图2
图2
(Ⅱ)tanθ=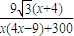 =
=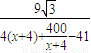 ,x>0.
,x>0.
因为4(x+4)+ -41≥2
-41≥2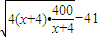 =39,当且仅当4(x+4)=
=39,当且仅当4(x+4)=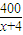 ,即x=6时取等号.
,即x=6时取等号.
所以当x=6时,4(x+4)+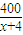 -41取最小值39.
-41取最小值39.
所以当x=6时,tanθ取最大值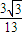 .
.
由于y=tanx在区间(0, )上是增函数,所以当x=6时,θ取得最大值.
)上是增函数,所以当x=6时,θ取得最大值.
答:在海湾一侧的海岸线CT上距C点6km处的D点处观看飞机跑道的视角最大.
点评:考查学生根据实际问题选择函数类型的能力.
 求出其值即可.
求出其值即可.(Ⅱ)根据
 当且仅当a=b时取等号的方法,求出tanθ的最大值,根据正切函数是单调增函数得到x的值表示出D的位置即可.
当且仅当a=b时取等号的方法,求出tanθ的最大值,根据正切函数是单调增函数得到x的值表示出D的位置即可.解答:解:(Ⅰ)过A分别作直线CD,BC的垂线,垂足分别为E,F.由题可知,AB=4.5,BC=4
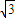 ,∠ABF=90°-60°=30°,
,∠ABF=90°-60°=30°,所以CE=AF=4.5×sin30°=
 ,BF=4.5×cos30°=
,BF=4.5×cos30°=
 ,AE=CF=BC+BF=
,AE=CF=BC+BF=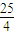
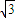 .
.因为CD=x(x>0).所以tan∠BDC=
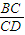 =
=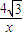 .
.当x>
 时,ED=x-
时,ED=x- ,tan∠ADC=
,tan∠ADC=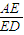 =
=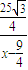 =
=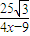 (如图1).
(如图1).当0<x<
 时,ED=
时,ED= -x,tan∠ADC=
-x,tan∠ADC=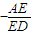 =
=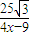 (如图2).
(如图2).所以tanθ=tan∠ADB=tan(∠ADC-∠BDC)=
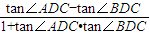 =
= =
= ,其中x>0且x≠
,其中x>0且x≠ .
.当x=
 时,tanθ=
时,tanθ= =
=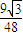 ,符合上式.
,符合上式.所以tanθ=
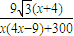 .x>0
.x>0图1
 图2
图2
(Ⅱ)tanθ=
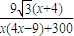 =
=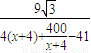 ,x>0.
,x>0.因为4(x+4)+
 -41≥2
-41≥2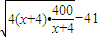 =39,当且仅当4(x+4)=
=39,当且仅当4(x+4)=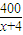 ,即x=6时取等号.
,即x=6时取等号.所以当x=6时,4(x+4)+
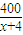 -41取最小值39.
-41取最小值39.所以当x=6时,tanθ取最大值
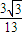 .
.由于y=tanx在区间(0,
 )上是增函数,所以当x=6时,θ取得最大值.
)上是增函数,所以当x=6时,θ取得最大值.答:在海湾一侧的海岸线CT上距C点6km处的D点处观看飞机跑道的视角最大.
点评:考查学生根据实际问题选择函数类型的能力.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
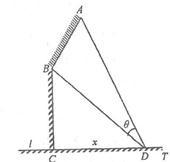 如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60°(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60°(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4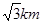 ,D为海岸线l上的一点.设CD=xkm(x>
,D为海岸线l上的一点.设CD=xkm(x> ),点D对跑道AB的视角为
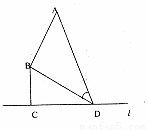
),点D对跑道AB的视角为 .
.
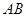 的长为4.5
的长为4.5 ,且跑道所在的直线与海岸线
,且跑道所在的直线与海岸线 的夹角为
的夹角为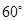 (海岸线可以看作是直线),跑道上离海岸线距离最近的点
(海岸线可以看作是直线),跑道上离海岸线距离最近的点 到海岸线的距离
到海岸线的距离 .
.
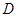 为海湾一侧海岸线
为海湾一侧海岸线 上的一点,设
上的一点,设 ,点
,点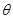 .
.
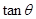 表示为
表示为 的函数;
的函数; ,对于任意的
,对于任意的 ,
,
 ,等号成立当
,等号成立当 ,求点
,求点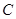 的位置,使
的位置,使 如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60度(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60度(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离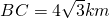 . D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为θ.
. D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为θ.