题目内容
(文科)点M是圆x2+y2=4上的一个动点,过点M作MD垂直于x轴,垂足为D,P为线段MD的中点.
(1)求点P的轨迹方程;
(2)设点P的轨迹为C,若直线l:y=-ex+m(其中e为曲线C的离心率)与曲线C有两个不同的交点A与B且
•
=2(其中O为坐标原点),求m的值.
(1)求点P的轨迹方程;
(2)设点P的轨迹为C,若直线l:y=-ex+m(其中e为曲线C的离心率)与曲线C有两个不同的交点A与B且
| OA |
| OB |
(1)由题意,令P(x,y),
则由中点坐标公式知:D(x,0),M(x,2y),
∵点M是圆x2+y2=4上的一个动点,
∴点P的轨迹方程为x2+4y2=4.
(2)由(1)点P的轨迹是椭圆x2+4y2=4,
∴e=
.
∵直线l:y=-
x+m与曲线C:x2+4y2=4有两个不同的交点A与B,
∴
?x2-
mx+m2-1=0有两个解,
∴△=-m2+4>0,∴-2<m<2.
设A(x1,y1),B(x2,y2),x1+x2=
m,x1x2=m2-1,
∵
•
=2(其中O为坐标原点),
∴x1x2+y1y2=2,
∴5m2=7,∴m=±
.
则由中点坐标公式知:D(x,0),M(x,2y),
∵点M是圆x2+y2=4上的一个动点,
∴点P的轨迹方程为x2+4y2=4.
(2)由(1)点P的轨迹是椭圆x2+4y2=4,
∴e=
| ||
| 2 |
∵直线l:y=-
| ||
| 2 |
∴
|
| 3 |
∴△=-m2+4>0,∴-2<m<2.
设A(x1,y1),B(x2,y2),x1+x2=
| 3 |
∵
| OA |
| OB |
∴x1x2+y1y2=2,
∴5m2=7,∴m=±
| ||
| 5 |

练习册系列答案
相关题目
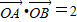 (其中O为坐标原点),求m的值.
(其中O为坐标原点),求m的值.