题目内容
(本大题9分)袋中有2个红球,n个白球,各球除颜色外均相同.已知从袋中摸出2个球均为白球的概率为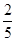 ,(Ⅰ)求n;(Ⅱ)从袋中不放回的依次摸出三个球,记ξ为相邻两次摸出的球不同色的次数(例如:若取出的球依次为红球、白球、白球,则ξ=1),求随机变量ξ的分布列及其数学期望Eξ.
,(Ⅰ)求n;(Ⅱ)从袋中不放回的依次摸出三个球,记ξ为相邻两次摸出的球不同色的次数(例如:若取出的球依次为红球、白球、白球,则ξ=1),求随机变量ξ的分布列及其数学期望Eξ.
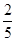 ,(Ⅰ)求n;(Ⅱ)从袋中不放回的依次摸出三个球,记ξ为相邻两次摸出的球不同色的次数(例如:若取出的球依次为红球、白球、白球,则ξ=1),求随机变量ξ的分布列及其数学期望Eξ.
,(Ⅰ)求n;(Ⅱ)从袋中不放回的依次摸出三个球,记ξ为相邻两次摸出的球不同色的次数(例如:若取出的球依次为红球、白球、白球,则ξ=1),求随机变量ξ的分布列及其数学期望Eξ.(1)n=4
(2)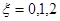
P(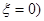 =
=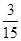 P(
P(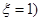 =
=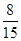
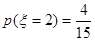 Eξ=
Eξ=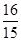
(2)
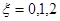
P(
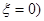 =
=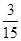 P(
P(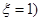 =
=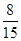
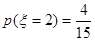 Eξ=
Eξ=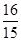
(I)由于每个球被摸到的机会是均等的,故可用古典概型的概率公式解答.
(II)ξ为相邻两次摸出的球不同色的次数,则随机变量ξ的取值为0,1,2,利用古典概型的概率公式求出相应的概率,进而可得ξ的分布列及其数学期望Eξ.
(II)ξ为相邻两次摸出的球不同色的次数,则随机变量ξ的取值为0,1,2,利用古典概型的概率公式求出相应的概率,进而可得ξ的分布列及其数学期望Eξ.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 ,求
,求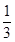 ,将赝品错误地鉴定为正品的概率为
,将赝品错误地鉴定为正品的概率为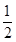 ,已知一批物品共有4件,其中正品3件,赝品1件.(1)求该收藏爱好者的鉴定结果为正品2件,赝品2件的概率;(2)求该收藏爱好者的鉴定结果中正品数
,已知一批物品共有4件,其中正品3件,赝品1件.(1)求该收藏爱好者的鉴定结果为正品2件,赝品2件的概率;(2)求该收藏爱好者的鉴定结果中正品数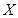 的分布列及数学期望.
的分布列及数学期望.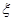 的分布列如下:
的分布列如下: ,则y的值为 .
,则y的值为 .
 三个社区中各选一人,求恰好有2人是低碳族的概率;
三个社区中各选一人,求恰好有2人是低碳族的概率;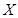 为选出的4名选手中女选手的人数,求
为选出的4名选手中女选手的人数,求 (元)
(元)
 (元)
(元)