题目内容
某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是
| A.72 | B.120 | C.144 | D.168 |
B
解析试题分析:将所有的安排方法分成两类,第一类:歌舞类节目中间不穿插相声节目,
有 (种);
(种);
第二类:歌舞类节目中间穿插相声节目,有 (种);
(种);
根据分类加法计数原理,共有96+24=120种不同的排法.
故选B.
考点:1、分类加法计数原理;2、排列.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
一名老师和两名男生两名女生站成一排照相,要求两名女生必须站在一起且老师不站在两端,则不同站法的种数为( ).
| A.8 | B.12 | C.16 | D.24 |
有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( )
| A.60种 | B.70种 | C.75种 | D.150种 |
设函数 ,其中
,其中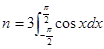 ,则
,则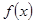 的展开式中
的展开式中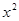 的系数为( )
的系数为( )
A. | B.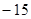 | C.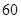 | D.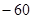 |
若(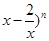 的展开式中第2项与第4项的二项式系数相等,则直线y=nx与曲线y=x2围成的封闭区域面积为( )
的展开式中第2项与第4项的二项式系数相等,则直线y=nx与曲线y=x2围成的封闭区域面积为( )
A.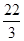 | B.12 | C.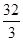 | D.36 |
若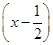 n的展开式中第3项的二项式系数是15,则展开式中所有项系数之和为( )
n的展开式中第3项的二项式系数是15,则展开式中所有项系数之和为( )
A.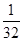 | B.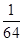 | C.-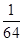 | D.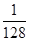 |
将A,B,C,D,E排成一列,要求A,B,C在排列中顺序为“A,B,C”或“C,B,A”(可以不相邻),这样的排列数有( )
| A.12种 | B.20种 | C.40种 | D.60种 |
从1,3,5,7,9这五个数中,每次取出两个不同的数分别记为a,b,共可得到lga-lgb的不同值的个数是( )
| A.9 |
| B.10 |
| C.18 |
| D.20 |
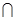 B={1,3,5},则称A,B为“理想配集”,记作(A,B),问这样的“理想配集”(A,B)共有( )
B={1,3,5},则称A,B为“理想配集”,记作(A,B),问这样的“理想配集”(A,B)共有( )