题目内容
观察下列式子：1+| 1 |
| 22 |
| 3 |
| 2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 5 |
| 3 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 7 |
| 4 |
分析：观察发现，右边是正整数（n）的平方的倒数和，左边是分子是正奇数，分母是正整数n，然后可以猜想的结论为：当n∈N且n≥2时的不等式子．
解答：解：根据规律，右边是正整数（n）的平方的倒数和，左边是分子是正奇数，分母是正整数n，
可以猜想的结论为：当n∈N且n≥2时，恒有1+
+
+…+
＜
故答案为1+
+
+…+
＜
可以猜想的结论为：当n∈N且n≥2时，恒有1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 2n-1 |
| n |
故答案为1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 2n-1 |
| n |
点评：本题利用平方差公式考查了数字变化规律的问题，求出左边两底数是解题的关键．
练习册系列答案
口算能手系列答案
相关题目
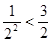,1+
＜
,1+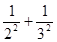
,…
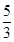,1+
,1+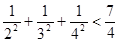
,…,由此猜想一个一般性的结论，并加以证明.