题目内容
对任意正整数x,y都有f(x+y)=f(x)•f(y),且f(1)= ,则
,则 [f(1)+f(2)+f(3)+…+f(n)]=( )
[f(1)+f(2)+f(3)+…+f(n)]=( )A.

B.1
C.-

D.

【答案】分析:先由f (x+y)=f (x)•f (y)得f (2x)=f (x)2⇒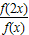 =f(x).以及
=f(x).以及 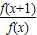 =
= ,两个结论相结合可得
,两个结论相结合可得 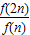 =f(n)=
=f(n)=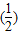 n,把问题转化为求等比数列的和,再代入求和公式即可.
n,把问题转化为求等比数列的和,再代入求和公式即可.
解答:解:由f(x+y)=f(x)•f(y)得 f(2x)=f(x)2⇒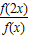 =f(x).
=f(x).
∵f (x+y)=f (x)•f (y)⇒f (x+1)=f (x)•f (2)=2f(x)⇒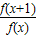 =
= ,
,
所以数列{f(n)}是以 为首项,
为首项, 为公比的等比数列,故f(n)=
为公比的等比数列,故f(n)= ×
× n-1=(
n-1=( )n.
)n.
∴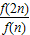 =f(n)=(
=f(n)=( )n.
)n.
则 f(1)+f(2)+f(3)+…+f(n)]=( )1+(
)1+( )2+(
)2+( )3+…+
)3+…+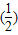 n=
n=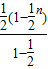 =1-(
=1-( )n.
)n.
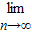 [f(1)+f(2)+f(3)+…+f(n)]=
[f(1)+f(2)+f(3)+…+f(n)]=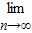 [1-(
[1-( )n]=1
)n]=1
故选B.
点评:本题主要考查抽象函数及其应用.抽象函数是相对于给出具体解析式的函数来说的,它虽然没有具体的表达式,但是有一定的对应法则,满足一定的性质,这种对应法则及函数的相应的性质是解决问题的关键.
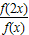 =f(x).以及
=f(x).以及 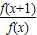 =
= ,两个结论相结合可得
,两个结论相结合可得 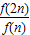 =f(n)=
=f(n)=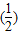 n,把问题转化为求等比数列的和,再代入求和公式即可.
n,把问题转化为求等比数列的和,再代入求和公式即可.解答:解:由f(x+y)=f(x)•f(y)得 f(2x)=f(x)2⇒
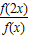 =f(x).
=f(x).∵f (x+y)=f (x)•f (y)⇒f (x+1)=f (x)•f (2)=2f(x)⇒
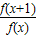 =
= ,
,所以数列{f(n)}是以
 为首项,
为首项, 为公比的等比数列,故f(n)=
为公比的等比数列,故f(n)= ×
× n-1=(
n-1=( )n.
)n.∴
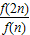 =f(n)=(
=f(n)=( )n.
)n.则 f(1)+f(2)+f(3)+…+f(n)]=(
 )1+(
)1+( )2+(
)2+( )3+…+
)3+…+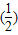 n=
n=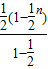 =1-(
=1-( )n.
)n.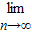 [f(1)+f(2)+f(3)+…+f(n)]=
[f(1)+f(2)+f(3)+…+f(n)]=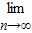 [1-(
[1-( )n]=1
)n]=1故选B.
点评:本题主要考查抽象函数及其应用.抽象函数是相对于给出具体解析式的函数来说的,它虽然没有具体的表达式,但是有一定的对应法则,满足一定的性质,这种对应法则及函数的相应的性质是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
对任意正整数x,y都有f(x+y)=f(x)•f(y),且f(1)=
,则f(1)+f(2)+…+f(2011)=( )
| 1 |
| 2 |
A、1-
| ||
B、1-
| ||
C、1-
| ||
D、
|
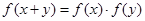 ,且
,且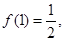 则
则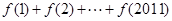 =
(
)
=
(
)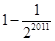 B.
B.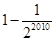 C.
C. D.
D. 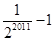 [来源:]
[来源:]