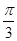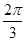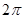题目内容
在正三棱锥S-ABC中,外接球的表面积为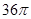 ,M,N分别是SC,BC的中点,且
,M,N分别是SC,BC的中点,且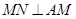 ,则此三棱锥侧棱SA=( )
,则此三棱锥侧棱SA=( )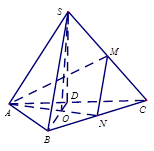
| A.1 | B.2 | C.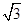 | D. |
D
解析试题分析:作SO⊥平面ABC,O为三角形ABC的重心.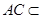 平面ABC,SO⊥AC. 作BO交AC于点D.所以AC⊥BD.又
平面ABC,SO⊥AC. 作BO交AC于点D.所以AC⊥BD.又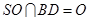 .所以AC⊥SB.又因为M,N分别是中点,所以MN∥SB,又因为MN⊥AM.所以AM⊥SB.又因为
.所以AC⊥SB.又因为M,N分别是中点,所以MN∥SB,又因为MN⊥AM.所以AM⊥SB.又因为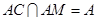 .所以SB⊥平面SAC.又因为三棱锥S-ABC是正三棱锥,所以SA,SB,SC之间两两垂直.通过补齐为一个正方体,则正方体的外接球的直径为6,则正方体的棱长为
.所以SB⊥平面SAC.又因为三棱锥S-ABC是正三棱锥,所以SA,SB,SC之间两两垂直.通过补齐为一个正方体,则正方体的外接球的直径为6,则正方体的棱长为 .满足
.满足 .故选D.
.故选D.
考点:1.球的表面积.2.割补法的思想.3.线线、线面位置关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
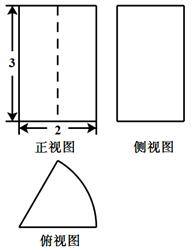
已知某几何体的三视图(单位: )如图所示,则此几何体的体积是( )
)如图所示,则此几何体的体积是( )
A.1  | B.3 | C.5 | D.7 |
一个机器零件的三视图如图所示,其中俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为( )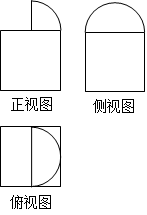
A.8+ | B.8+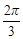 |
C.8+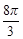 | D.8+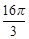 |
如图所示是一个几何体的三视图,若该几何体的体积为 ,则主视图中三角形的高x的值为( )
,则主视图中三角形的高x的值为( )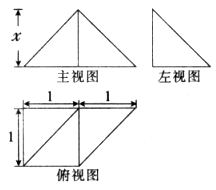
A. | B.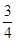 | C.1 | D.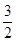 |
一个几何体的三视图如图所示(单位:cm),则该几何体的表面积为( )
| A.54cm2 | B.91cm2 | C.75+4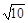 cm2 cm2 | D.75+2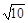 cm2 cm2 |
某圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于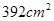 ,母线与轴的夹角为
,母线与轴的夹角为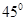 ,则这个圆台的高为
,则这个圆台的高为
| A.7 | B.14 | C.21 | D. |
某几何体的三视图如图所示,则该几何体的表面积为( ).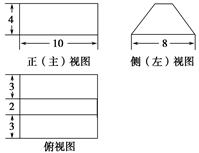
| A.180 | B.200 | C.220 | D.240 |


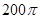

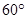 的扇形,则该几何体的体积为( )
的扇形,则该几何体的体积为( )