题目内容
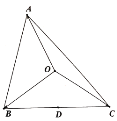
【题目】将平面上每个点都以红、蓝两色之一着色,证明:存在这样的两个相似三角形,它们的相似比为1995,并且每一个三角形的三个顶点同色。
【答案】见解析
【解析】
首先证明平面上一定存在三顶点同色的直角三角形.在平面上任作直线![]() ,则
,则![]() 上必有两点同色,设此两点为
上必有两点同色,设此两点为![]() ,
,![]() .过
.过![]() ,
,![]() 分别作
分别作![]() 的垂线
的垂线![]() ,
,![]() .如果
.如果![]() 或
或![]() 上有与
上有与![]() ,
,![]() 同色的点
同色的点![]() ,则
,则
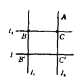
![]() 即为三顶点同色的直角三角形.如果
即为三顶点同色的直角三角形.如果![]() 与
与![]() 上除
上除![]() 与
与![]() 外其余点均与
外其余点均与![]() ,
,![]() 异色,则在
异色,则在![]() 上取异于
上取异于![]() 的两点
的两点![]() ,
,![]() ,并过
,并过![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() 即为三顶点同色的直角三角形.因此,平面上一定存在三顶点同色的直角三角形,设其中之一为
即为三顶点同色的直角三角形.因此,平面上一定存在三顶点同色的直角三角形,设其中之一为![]() .将
.将![]() 对称地补成矩形
对称地补成矩形![]() .用两组分别平行于
.用两组分别平行于![]() 与
与![]() 的
的![]() 等分平行线将矩形
等分平行线将矩形![]() 等分成
等分成![]() 个与原矩形相似的小矩形.(如图)
个与原矩形相似的小矩形.(如图)
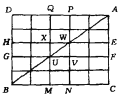
以下用反证法证明:若![]() 为奇数,则在这些小矩形中必有一个,它的顶点中至少有三个同色,即存在一个三顶点同色的小直角三角形.假设不存在三顶点同色的小直角三角形.线段
为奇数,则在这些小矩形中必有一个,它的顶点中至少有三个同色,即存在一个三顶点同色的小直角三角形.假设不存在三顶点同色的小直角三角形.线段![]() 上端点及分点共
上端点及分点共![]() 个,
个,![]() 为偶数,因此
为偶数,因此![]() 上必有相邻的两点同色(若每相邻两点异色,则
上必有相邻的两点同色(若每相邻两点异色,则![]() ,
,![]() 亦应异色,与已知矛盾),不妨设为
亦应异色,与已知矛盾),不妨设为![]() ,
,![]() .则
.则![]() ,
,![]() 所在的小矩形的另两个顶点必与
所在的小矩形的另两个顶点必与![]() ,
,![]() 异色(否则已出现同色小三角形).依次类推,可知矩形
异色(否则已出现同色小三角形).依次类推,可知矩形![]() 中,每条竖线上的两顶点都同色.同理,线段
中,每条竖线上的两顶点都同色.同理,线段![]() 上有相邻两点
上有相邻两点![]() ,
,![]() 同色,也有矩形
同色,也有矩形![]() ,其中每条横线上的两顶点都同色.设矩形
,其中每条横线上的两顶点都同色.设矩形![]() 与
与![]() 的公共部分为小矩形
的公共部分为小矩形![]() ,由以上所说,
,由以上所说,![]() 与
与![]() 同色且
同色且![]() 与
与![]() 同色,从而
同色,从而![]() 即是三顶点同色的小直角三角形.这与假设矛盾.因此必存在一个三顶点同色的小直角三角形.这个三顶点同色的小直角三角形与原直角三角形是相似的,相似比为
即是三顶点同色的小直角三角形.这与假设矛盾.因此必存在一个三顶点同色的小直角三角形.这个三顶点同色的小直角三角形与原直角三角形是相似的,相似比为![]() ,当
,当![]() 时就是题目所要证明的结论.
时就是题目所要证明的结论.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某果农从经过筛选(每个水果的大小最小不低于50克,最大不超过100克)的10000个水果中抽取出100个样本进行统计,得到如下频率分布表:
级别 | 大小(克) | 频数 | 频率 |
一级果 |
| 5 | 0.05 |
二级果 |
|
| |
三级果 |
| 35 |
|
四级果 |
| 30 | |
五级果 |
| 20 | |
合计 | 100 |
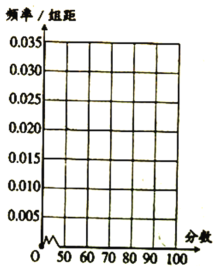
请根据频率分布表中所提供的数据,解得下列问题:
(1)求![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
(2)若从四级果,五级果中按分层抽样的方法抽取5个水果,并从中选出2个作为展品,求2个展品中仅有1个是四级果的概率;
(3)若将水果作分级销售,预计销售的价格![]() 元/个与每个水果的大小
元/个与每个水果的大小![]() 克关系是:
克关系是: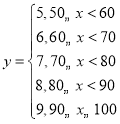 ,则预计10000个水果可收入多少元?
,则预计10000个水果可收入多少元?