题目内容
已知O为锐角△ABC的外心,AB=6,AC=10,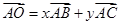 ,且2x+10y=5,则边BC的长
,且2x+10y=5,则边BC的长
为.
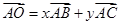 ,且2x+10y=5,则边BC的长
,且2x+10y=5,则边BC的长为.
4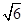
分别取AB、AC的中点D、E,连结OD、OE,∵O是锐角△ABC的外接圆的圆心,D、E分别为AB、AC的中点,∴OD⊥AB,OE⊥AC.由此可得在Rt△AOD中,cos∠OAD=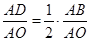 ,
,
∴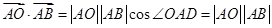
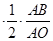 =
=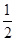
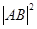 =18.
=18.
同理可得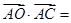
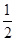
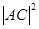 =50.
=50.
∵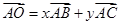 ,
,
∴等式的两边都与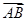 作数量积,得
作数量积,得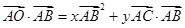 ,化简得18=36x+y
,化简得18=36x+y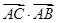 , ①
, ①
同理,等式的两边都与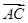 作数量积,化简得50=x
作数量积,化简得50=x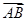
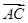 +100y, ②
+100y, ②
又∵根据题意知2x+10y=5, ③
∴①②③联解,可得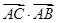 =20,x=
=20,x=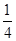 且y=
且y=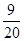 .
.
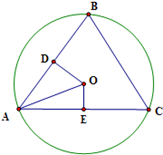
∴AC·ABcos∠A=20,即10×6cos∠A=20,cos∠A=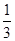 ,
,
由余弦定理得,BC2=AB2+AC2-2AB·ACcos∠A=96,BC=4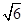 .
.
【考点】1.三角形外接圆的性质;2.锐角的三角函数在直角三角形中的定义;3.向量量的数量积公式和方程组的解法.
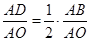 ,
,∴
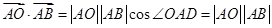
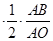 =
=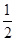
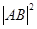 =18.
=18.同理可得
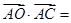
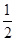
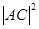 =50.
=50.∵
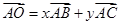 ,
,∴等式的两边都与
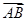 作数量积,得
作数量积,得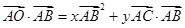 ,化简得18=36x+y
,化简得18=36x+y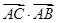 , ①
, ①同理,等式的两边都与
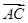 作数量积,化简得50=x
作数量积,化简得50=x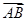
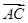 +100y, ②
+100y, ②又∵根据题意知2x+10y=5, ③
∴①②③联解,可得
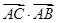 =20,x=
=20,x=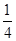 且y=
且y=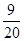 .
.
∴AC·ABcos∠A=20,即10×6cos∠A=20,cos∠A=
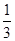 ,
,由余弦定理得,BC2=AB2+AC2-2AB·ACcos∠A=96,BC=4
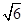 .
.【考点】1.三角形外接圆的性质;2.锐角的三角函数在直角三角形中的定义;3.向量量的数量积公式和方程组的解法.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
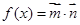 ,其中向量
,其中向量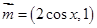 ,
,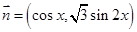 ,
,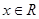 .
.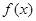 的单调递增区间;
的单调递增区间;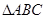 中,
中,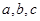 分别是角
分别是角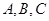 的对边,已知
的对边,已知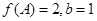 ,
,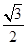 ,求
,求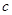 的值.
的值. .
.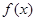 的单调减区间;
的单调减区间;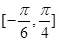 上最大值和最小值.
上最大值和最小值.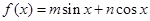 ,且
,且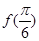 是它的最大值,(其中m、n为常数且
是它的最大值,(其中m、n为常数且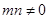 )给出下列命题:①
)给出下列命题:①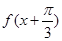 是偶函数;②函数
是偶函数;②函数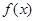 的图象关于点
的图象关于点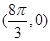 对称;③
对称;③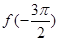 是函数
是函数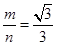 .
.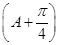 =
=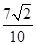 ,A∈
,A∈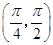 .
.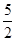 sinAsinx的值域.
sinAsinx的值域.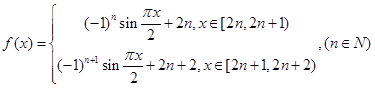 ,若数列
,若数列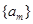 满足
满足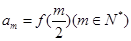 ,且
,且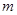 项和为
项和为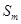 ,则
,则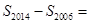 _____________.
_____________.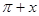 )>0成立的x的取值范围为( )
)>0成立的x的取值范围为( )