题目内容
((本题16分)
(1)用红、黄、蓝、白四种不同颜色的鲜花布置如图一所示的花圃,要求同一区域上用同一种颜色鲜花,相邻区域用不同颜色鲜花,问共有多少种不同的摆放方案?
(2)用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图二所示的花圃,要求同一区域上用同一种颜色鲜花,相邻区域使用不同颜色鲜花.

①求恰有两个区域用红色鲜花的概率;
②记花圃中红色鲜花区域的块数为S,求它的分布列及其数学期望E(S).
【答案】
(1)根据分步计数原理,摆放鲜花的不同方案有: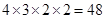 种.、、、、、、 6分
种.、、、、、、 6分
(2)① 设M表示事件“恰有两个区域用红色鲜花”,
如图二,当区域A、D同色时,共有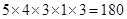 种;
种;
当区域A、D不同色时,共有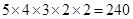 种;因此,所有基本事件总数为:180+240=420种.(由于只有A、D,B、E可能同色,故可按选用3色、4色、5色分类计算,求出基本事件总数为
种;因此,所有基本事件总数为:180+240=420种.(由于只有A、D,B、E可能同色,故可按选用3色、4色、5色分类计算,求出基本事件总数为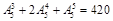 种)它们是等可能的。又因为A、D为红色时,共有
种)它们是等可能的。又因为A、D为红色时,共有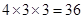 种;B、E为红色时,共有
种;B、E为红色时,共有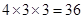 种;因此,事件M包含的基本事件有:36+36=72种.所以,
种;因此,事件M包含的基本事件有:36+36=72种.所以,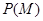 =
=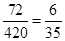 . 、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、12分
. 、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、12分
②随机变量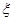 的分布列为:
的分布列为:
|
|
0 |
1 |
2 |
|
P |
|
|
|
所以,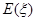 =
= .、、、、、、、、、、、、、、、、、、、、、、、、16分
.、、、、、、、、、、、、、、、、、、、、、、、、16分
【解析】略

练习册系列答案
相关题目
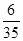
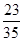
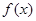 满足满足
满足满足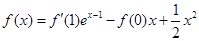 ;
;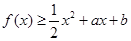 ,求
,求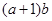 的最大值.
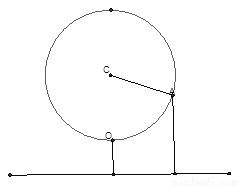
的最大值. 离地面1米,风车圆周上一点A从最底点
离地面1米,风车圆周上一点A从最底点
 ,
,
 轴的正向,OB为
轴的正向,OB为 轴正向,建立直角坐标系,求出斜坡CD所在直线方程;
轴正向,建立直角坐标系,求出斜坡CD所在直线方程;