题目内容
在等差数列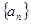 中,前四项之和为40,最后四项之和为80,所有项之和是210,则项数
中,前四项之和为40,最后四项之和为80,所有项之和是210,则项数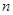 为( )
为( )
A.12 B.14 C.15 D.16
【答案】
B
【解析】
试题分析:由题意可得,a1+a2+a3+a4=40①an+an-1+an-2+an-3=80②
由等差数列的性质可知①+②可得,4(a1+an)=120⇒(a1+an)=30
由等差数列的前n项和公式可得,Sn= = 15n=210,所以n=14,故选B.
= 15n=210,所以n=14,故选B.
考点:本试题主要考查了等差数列的性质,等差数列的前n项和公式的简单运用,属于对基础知识的简单综合.
点评:解决该试题的关键是由题意可得,a1+a2+a3+a4=40,an+an-1+an-2+an-3=80,两式相加且由等差数列的性质可求(a1+an)代入等差数列的前n项和公式得到结论。

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
在等差数列 中,前四项之和为60,最后四项之和为100,所有项之和是120,则项数
中,前四项之和为60,最后四项之和为100,所有项之和是120,则项数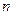 为( )
为( )
| A.3 | B.4 | C.5 | D.6 |
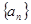 中,前四项之和为60,最后四项之和为100,所有项之和是120,则项数
中,前四项之和为60,最后四项之和为100,所有项之和是120,则项数 为( )
为( )