题目内容
设椭圆C1和抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表中:
(Ⅰ)求曲线C1,C2的标准方程;
(Ⅱ)设直线l与椭圆C1交于不同两点M、N,且
•
=0,请问是否存在直线l过抛物线C2的焦点F?若存在,求出直线l的方程;若不存在,请说明理由.
| x | 3 | -2 | 4 |
| ||||||
| y | -2
|
0 | -4 |
|
(Ⅱ)设直线l与椭圆C1交于不同两点M、N,且
| OM |
| ON |
分析:(I)由题意(-2,0),一定在椭圆C1上,设C1方程为
+
=1(a>b>0),可得a=2.于是椭圆C1上任何点的横坐标|x|≤2.可判断点(
,
)也在C1上,代入椭圆方程即可解得b2,因此得到椭圆的方程.从而(3,-2
),(4,-4)一定在抛物线C2上,设C2的方程为y2=2px(p>0),把其中一个点的坐标代入即可得出.
(II)假设直线l过C2的焦点F(1,0).分类讨论:当l的斜率不存在时,得出M,N的坐标,然后验证是否满足
•
=0,即可.
当l的斜率存在时设为k,则l的方程为y=k(x-1)代入C1方程并整理可得根与系数的关系,利用
•
=0,可得k的值即可.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
| 3 |
(II)假设直线l过C2的焦点F(1,0).分类讨论:当l的斜率不存在时,得出M,N的坐标,然后验证是否满足
| OM |
| ON |
当l的斜率存在时设为k,则l的方程为y=k(x-1)代入C1方程并整理可得根与系数的关系,利用
| OM |
| ON |
解答:解:(I)由题意(-2,0),一定在椭圆C1上,
设C1方程为
+
=1(a>b>0),则a=2,
∴椭圆C1上任何点的横坐标|x|≤2.
∴(
,
)也在C1上,代入椭圆方程
+
=1,
解得b2=1,
∴C1的方程为
+y2=1.
从而(3,-2
),(4,-4)一定在抛物线C2上,
设C2的方程为y2=2px(p>0),可得(-4)2=2p×4.
∴p=2,即C2的方程为y2=4x.
(II)假设直线l过C2的焦点F(1,0).
当l的斜率不存在时,则M(1,
),N(1,-
).
此时
•
=1-
=
≠0,与已知矛盾.
当l的斜率存在时设为k,则l的方程为y=k(x-1)代入C1方程并整理得,(1+4k2)x2-8k2x+4k2-4=0.
∵直线l过椭圆内部(1,0)点,故必有两交点.
设M(x1,y1),N(x2,y2),则
x1+x2=
,x1x2=
.
y1y2=k(x1-1)k(x2-1)=k2(x1x2-x1-x2+1)
=
,
∵
•
=0,∴x1x2+y1y2=0,
∴k2-4=0,k=±2,
∴存在符合条件的直线l且方程为y=±2(x-1).
设C1方程为
| x2 |
| a2 |
| y2 |
| b2 |
∴椭圆C1上任何点的横坐标|x|≤2.
∴(
| 2 |
| ||
| 2 |
(
| ||
| 22 |
(
| ||||
| b2 |
解得b2=1,
∴C1的方程为
| x2 |
| 4 |
从而(3,-2
| 3 |
设C2的方程为y2=2px(p>0),可得(-4)2=2p×4.
∴p=2,即C2的方程为y2=4x.
(II)假设直线l过C2的焦点F(1,0).
当l的斜率不存在时,则M(1,
| ||
| 2 |
| ||
| 2 |
此时
| OM |
| ON |
| 3 |
| 4 |
| 1 |
| 4 |
当l的斜率存在时设为k,则l的方程为y=k(x-1)代入C1方程并整理得,(1+4k2)x2-8k2x+4k2-4=0.
∵直线l过椭圆内部(1,0)点,故必有两交点.
设M(x1,y1),N(x2,y2),则
x1+x2=
| 8k2 |
| 1+4k2 |
| 4k2-4 |
| 1+4k2 |
y1y2=k(x1-1)k(x2-1)=k2(x1x2-x1-x2+1)
=
| -3k2 |
| 1+4k2 |
∵
| OM |
| ON |
∴k2-4=0,k=±2,
∴存在符合条件的直线l且方程为y=±2(x-1).
点评:本题综合考查了椭圆与抛物线的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、数量积与向量垂直的关系等基础知识与基本技能方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
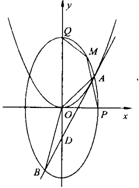 已知点D(0,-2),过点D作抛线C1:x2=2py(p>0)的切线l,切点A在第一象限,如图.
已知点D(0,-2),过点D作抛线C1:x2=2py(p>0)的切线l,切点A在第一象限,如图.