题目内容
已知等差数列{an}中,a3+a6=17,a1a8=﹣38且a1<a8.
(1)求{an}的通项公式;
(2)调整数列{an}的前三项a1、a2、a3的顺序,使它成为等比数列{bn}的前三项,求{bn}的前n项和.
(1)求{an}的通项公式;
(2)调整数列{an}的前三项a1、a2、a3的顺序,使它成为等比数列{bn}的前三项,求{bn}的前n项和.
解:(1)由已知,得求得a1=﹣2,a8=19
∴{an}的公差d=3
∴an=a1+(n﹣1)d=﹣2+3(n﹣1)=3n﹣5;
(2)由(1),得a3=a2+d=1+3=4,
∴a1=﹣2,a2=1,a3=4.
依题意可得:数列{bn}的前三项为b1=1,b2=﹣2,b3=4或b1=4,b2=﹣2,b3=1.
(i)当数列{bn}的前三项为b1=1,b2=﹣2,b3=4时,则q=﹣2,
∴ =
=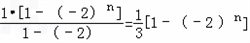
(ii)当数列{bn}的前三项为b1=4,b2=﹣2,b3=1时,则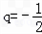 . ∴
. ∴ .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.