题目内容
已知椭圆C: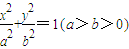 的离心率为
的离心率为 ,过坐标原点O且斜率为
,过坐标原点O且斜率为 的直线l与C相交于A,B,|AB|=
的直线l与C相交于A,B,|AB|=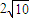 .
.(1)求a,b的值;
(2)若动圆(x-m)2+y2=1与椭圆C和直线l都没有公共点,试求m的取值范围.
【答案】分析:(1)依题意,l: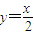 ,设A(2t,t)、B(-2t,t)(t>0),由|AB|=
,设A(2t,t)、B(-2t,t)(t>0),由|AB|=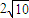 得20t2=40,
得20t2=40,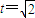 ,由此入手可解得a=4,b=2.
,由此入手可解得a=4,b=2.
(2)由题意知3x2-8mx+4m2+12=0,动圆与椭圆没有公共点,由此知|m|<3或|m|>5.再由动圆(x-m)2+y2=1与直线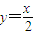 没有公共点.由此可得m的取值范围.
没有公共点.由此可得m的取值范围.
解答:解:(1)依题意,l: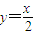 (1分)
(1分)
不妨设设A(2t,t)、B(-2t,-t)(t>0)(2分)
由|AB|=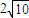 得20t2=40,
得20t2=40,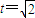 (3分)
(3分)
所以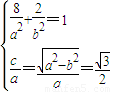 ((5分),)
((5分),)
解得a=4,b=2(6分).
(2)由 消去y得3x2-8mx+4m2+12=0(7分)
消去y得3x2-8mx+4m2+12=0(7分)
动圆与椭圆没有公共点,当且仅当△=(-8m)2-4×3×(4m2+12)=16m2-144<0或|m|>5(9分)
解得|m|<3或|m|>5(10分)
动圆(x-m)2+y2=1与直线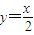 没有公共点当且仅当
没有公共点当且仅当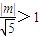 ,即|m|>
,即|m|>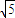 (12分)解
(12分)解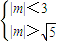 或
或 (13分)
(13分)
得m的取值范围为 .(14分)
.(14分)
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,仔细解答.
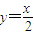 ,设A(2t,t)、B(-2t,t)(t>0),由|AB|=
,设A(2t,t)、B(-2t,t)(t>0),由|AB|=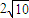 得20t2=40,
得20t2=40,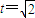 ,由此入手可解得a=4,b=2.
,由此入手可解得a=4,b=2.(2)由题意知3x2-8mx+4m2+12=0,动圆与椭圆没有公共点,由此知|m|<3或|m|>5.再由动圆(x-m)2+y2=1与直线
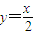 没有公共点.由此可得m的取值范围.
没有公共点.由此可得m的取值范围.解答:解:(1)依题意,l:
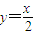 (1分)
(1分)不妨设设A(2t,t)、B(-2t,-t)(t>0)(2分)
由|AB|=
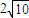 得20t2=40,
得20t2=40,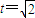 (3分)
(3分)所以
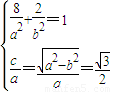 ((5分),)
((5分),)解得a=4,b=2(6分).
(2)由
 消去y得3x2-8mx+4m2+12=0(7分)
消去y得3x2-8mx+4m2+12=0(7分)动圆与椭圆没有公共点,当且仅当△=(-8m)2-4×3×(4m2+12)=16m2-144<0或|m|>5(9分)
解得|m|<3或|m|>5(10分)
动圆(x-m)2+y2=1与直线
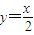 没有公共点当且仅当
没有公共点当且仅当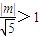 ,即|m|>
,即|m|>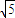 (12分)解
(12分)解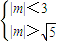 或
或 (13分)
(13分)得m的取值范围为
 .(14分)
.(14分)点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 的离心率为
的离心率为 ,且经过点
,且经过点 .
.
 的离心率为
的离心率为 ,过右焦点
,过右焦点 且斜率为
且斜率为 的直线与椭圆C相交于
的直线与椭圆C相交于 、
、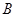 两点.若
两点.若 ,则
,则 =( )
=( )  B.
B. C.2
D.
C.2
D.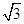
 ,它的离心率为
,它的离心率为 .直线
.直线 与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程.
与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程. 的离心率为
的离心率为 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
,椭圆C上任意一点到椭圆两个焦点的距离之和为6. :
: 与椭圆C交于
与椭圆C交于 ,
, 两点,点
两点,点 ,且
,且 ,求直线
,求直线