题目内容
给出下列说法:
①集合 ,则它的真子集有8个;
,则它的真子集有8个;
② 的值域为
的值域为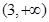 ;
;
③若函数 的定义域为
的定义域为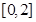 ,则函数
,则函数 的定义域为
的定义域为 ;
;
④函数 的定义在R上的奇函数,当
的定义在R上的奇函数,当 时,
时, ,则当
,则当 时,
时,
⑤设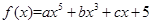 (其中
(其中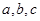 为常数,
为常数, ),若
),若 ,则
,则 ;其中正确的是 (只写序号)。
;其中正确的是 (只写序号)。
【答案】
②⑤
【解析】
试题分析:①集合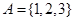 ,则它的真子集有
,则它的真子集有 个;
个;
③由函数 的定义域为
的定义域为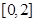 得:
得: ,解得
,解得 ;
;
④设 ,则
,则 ,所以
,所以 ,又因为
,又因为 是定义在R上的奇函数,所以
是定义在R上的奇函数,所以 =-
=-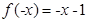 ;
;
⑤设g(x)= ,则g(x)是奇函数且
,则g(x)是奇函数且 =g(x)+5,因为
=g(x)+5,因为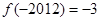 ,所以
,所以 ,所以
,所以 。
。
考点:本题考查真子集的性质、抽象函数的定义域、函数的奇偶性。
点评:此题主要考查集合子集个数的计算公式、函数的奇偶性和抽象函数定义域的求法,是一道基础题,若一个集合的元素个数为n,则其子集的个数为2n ,真子集的个数为2n-1个。

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
给出下列说法:
(1)
方程 的解集为{2,-2};
的解集为{2,-2};
(2)
集合 与{y|y=x-1,xÎR}的公共元素所组成的集合为{0,-1};
与{y|y=x-1,xÎR}的公共元素所组成的集合为{0,-1};
(3)
集合{x|x-1<0}与集合{x|x>a aÎR}没有公共元素.其中正确的个数为[
]|
A .0 |
B .1 |
C .2 |
D .3 |

 的解集为{2,-2};
的解集为{2,-2}; 与{y|y=x-1,xÎ
R}的公共元素所组成的集合为{0,-1};
与{y|y=x-1,xÎ
R}的公共元素所组成的集合为{0,-1}; 是同一个集合;
是同一个集合; ,则
,则 ;
; 与集合
与集合 表示同一个集合.
表示同一个集合.
 ;
;  ;
; 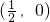 对称.
对称.