题目内容
设f (x)=sin 2x+ (sin
x-cos x)(sin x+cos x),其中x∈R.
(sin
x-cos x)(sin x+cos x),其中x∈R.
(Ⅰ) 该函数的图象可由
 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
(Ⅱ)若f (θ)= ,其中
,其中 ,求cos(θ+
,求cos(θ+ )的值;
)的值;
【答案】
(Ⅰ) 变换的步骤是:
①把函数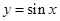 的图象向右平移
的图象向右平移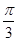 ,得到函数
,得到函数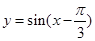 的图象;②令所得的图象上各点的纵坐标不变,把横坐标缩短到原来的
的图象;②令所得的图象上各点的纵坐标不变,把横坐标缩短到原来的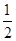 倍,得到函数
倍,得到函数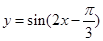 的图象;③令所得的图象上各点的横坐标不变,把纵坐标伸长到原来的2倍,得到函数
的图象;③令所得的图象上各点的横坐标不变,把纵坐标伸长到原来的2倍,得到函数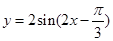 的图象.
的图象.
(Ⅱ) (1)当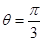 时,
时,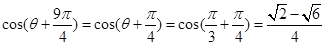 ;
;
(2)当 时;
时;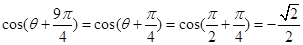 ;
;
【解析】解决正弦型函数如何由正弦函数变化而来的问题,可分两步:1变解析式2描述。
本题首先把函数f (x)=sin 2x+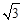 (sin
x-cos x)(sin x+cos x)化为正弦型函数
(sin
x-cos x)(sin x+cos x)化为正弦型函数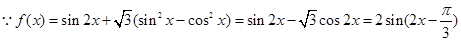 ;
;
变解析式: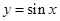
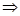
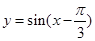
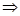
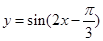
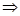
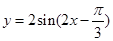
描述:
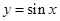

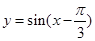

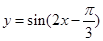
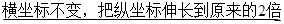
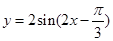
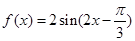 所以
所以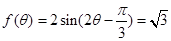 ,则
,则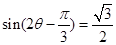 求得
求得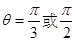 。
。
(Ⅰ) 解: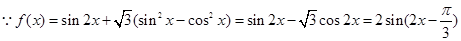
即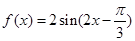 。…………………………………3分
。…………………………………3分
变换的步骤是:
①把函数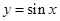 的图象向右平移
的图象向右平移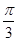 ,得到函数
,得到函数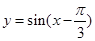 的图象;
的图象;
②令所得的图象上各点的纵坐标不变,把横坐标缩短到原来的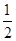 倍,得到函数
倍,得到函数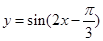 的图象;
的图象;
③令所得的图象上各点的横坐标不变,把纵坐标伸长到原来的2倍,得到函数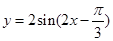 的图象;…………………………………3分
的图象;…………………………………3分
(Ⅱ) 解:因为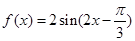 ,所以
,所以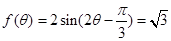 ,则
,则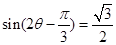 ,又
,又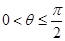
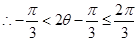 ,
,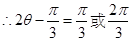 ,从而
,从而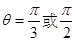 ……2分
……2分
(1)当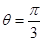 时,
时,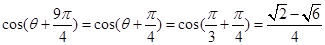 ;…………2分
;…………2分
(2)当 时;
时;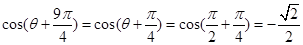 ;……………2分
;……………2分

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
 (sin x-cos x)(sin x+cos x),其中x∈R.
(sin x-cos x)(sin x+cos x),其中x∈R.
 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到? ,其中
,其中 ,求cos(θ+
,求cos(θ+ )的值;
)的值;
 变换分为三步,①把函数
变换分为三步,①把函数 ,得到函数
,得到函数 的图象;
的图象; 倍,得到函数
倍,得到函数 的图象;
的图象; 的图象;
的图象; ,则
,则 ,又
,又 ,
, ,从而
,从而

 时,
时, ;…………2分
;…………2分 时;
时;