题目内容
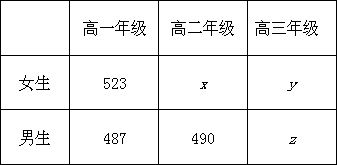某高级中学共有学生3000名，各年级男、女生人数如下表：已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.17．现对各年级用分层抽样的方法在全校抽取300名学生，则应在高三年级抽取分析：根据要在高二女生中抽取一个人的概率，做出高二女生的人数，用所有的人数减去高一和高二的人数，得到高三共有的人数，根据要抽取的人数和总体数，求出每个个体被抽到的概率，乘以高三的人数，得到结果．
解答：解：∵抽到高二年级女生的概率是0.17，
∴高二年级女生有0.17×3000=510，
∴高三年级共有3000-523-487-490-510=990，
∵对各年级用分层抽样的方法在全校抽取300名学生，
∴每个学生被抽到的概率是
=0.1，
∴应在高三抽取0.1×990=99
故答案为：99
∴高二年级女生有0.17×3000=510，
∴高三年级共有3000-523-487-490-510=990，
∵对各年级用分层抽样的方法在全校抽取300名学生，
∴每个学生被抽到的概率是
| 300 |
| 3000 |
∴应在高三抽取0.1×990=99
故答案为：99
点评：本题考查分层抽样方法，考查用样本的频率分布估计总体分布，本题是一个基础题，运算量不大，但是这种题目经常出现在试卷中．
练习册系列答案
相关题目
(13分) 某高级中学共有学生3 000名，各年级男、女生人数如下表：
| 高一年级 | 高二年级 | 高三年级 | |
| 男生 | 595 | 560 | y |
| 女生 | 605 | x | z |
已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.18.
(1)求x的值；
(2)现用分层抽样的方法在全校抽取120名学生，问应在高三年级抽取学生多少名？
(3)在(2)的前提下，已知y≥345，z≥345，求高三年级中男生比女生多的概率．
某高级中学共有学生3 000名，各年级男、女生人数如下表：
已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.18．
（1）求x的值；
（2）现用分层抽样的方法在全校抽取120名学生，问应在高三年级抽取学生多少名？
（3）在（2）的前提下，已知y≥345，z≥345，求高三年级中男生比女生多的概率．
| 高一年级 | 高二年级 | 高三年级 | |
| 男生 | 595 | 560 | y |
| 女生 | 605 | x | z |
（1）求x的值；
（2）现用分层抽样的方法在全校抽取120名学生，问应在高三年级抽取学生多少名？
（3）在（2）的前提下，已知y≥345，z≥345，求高三年级中男生比女生多的概率．
某高级中学共有学生3 000名，各年级男、女生人数如下表：
已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.18．
（1）求x的值；
（2）现用分层抽样的方法在全校抽取120名学生，问应在高三年级抽取学生多少名？
（3）在（2）的前提下，已知y≥345，z≥345，求高三年级中男生比女生多的概率．
| 高一年级 | 高二年级 | 高三年级 | |
| 男生 | 595 | 560 | y |
| 女生 | 605 | x | z |
（1）求x的值；
（2）现用分层抽样的方法在全校抽取120名学生，问应在高三年级抽取学生多少名？
（3）在（2）的前提下，已知y≥345，z≥345，求高三年级中男生比女生多的概率．