题目内容
某高级中学共有学生3 000名,各年级男、女生人数如下表:| 高一年级 | 高二年级 | 高三年级 | |
| 男生 | 595 | 560 | y |
| 女生 | 605 | x | z |
(1)求x的值;
(2)现用分层抽样的方法在全校抽取120名学生,问应在高三年级抽取学生多少名?
(3)在(2)的前提下,已知y≥345,z≥345,求高三年级中男生比女生多的概率.
【答案】分析:(1)根据在全校学生中随机抽取1名,抽到高二年级女生的概率是0.18建立等式,可求出x的值;
(2)先求出高三年级的人数,然后求出抽取比例,最后根据分层抽样的特点可求出应在高三年级抽取学生的人数;
(3)设高三年级男生比女生多的事件为A,高三年级男生、女生数记为(y,z),由(2)知y+z=700,且y,z∈N,y≥345,z≥345,列出基本事件空间包含的基本事件,以及事件A包含的基本事件,最后根据古典概型的概率公式解之即可.
解答:解:(1)∵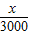 =0.18,∴x=540.…(3分)
=0.18,∴x=540.…(3分)
(2)高三年级人数为y+z=3000-(595+605+560+540)=700,
现用分层抽样的方法在全校抽取120名学生,
应在高三年级抽取的人数为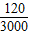 ×700=28名.…(7分)
×700=28名.…(7分)
(3)设高三年级男生比女生多的事件为A,高三年级男生、女生数记为(y,z).
由(2)知y+z=700,且y,z∈N,y≥345,z≥345.…(8分)
基本事件空间包含的基本事件有:(345,355)、(346,354)、(347,353)、(348,352)、(349,351)、(350,350)、(351,349)、(352,348)、(353,347)、(354,346)、(355,345)共11个,…(10分)
事件A包含的基本事件有:(351,349)、(352,348)、(353,347)、(354,346)、(355,345)共5个.
∴P(A)=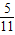 .…(13分)
.…(13分)
点评:本题主要考查了抽样方法中的分层抽样,以及古典概型的概率,同时考查了运算求解的能力,属于基础题.
(2)先求出高三年级的人数,然后求出抽取比例,最后根据分层抽样的特点可求出应在高三年级抽取学生的人数;
(3)设高三年级男生比女生多的事件为A,高三年级男生、女生数记为(y,z),由(2)知y+z=700,且y,z∈N,y≥345,z≥345,列出基本事件空间包含的基本事件,以及事件A包含的基本事件,最后根据古典概型的概率公式解之即可.
解答:解:(1)∵
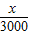 =0.18,∴x=540.…(3分)
=0.18,∴x=540.…(3分)(2)高三年级人数为y+z=3000-(595+605+560+540)=700,
现用分层抽样的方法在全校抽取120名学生,
应在高三年级抽取的人数为
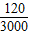 ×700=28名.…(7分)
×700=28名.…(7分)(3)设高三年级男生比女生多的事件为A,高三年级男生、女生数记为(y,z).
由(2)知y+z=700,且y,z∈N,y≥345,z≥345.…(8分)
基本事件空间包含的基本事件有:(345,355)、(346,354)、(347,353)、(348,352)、(349,351)、(350,350)、(351,349)、(352,348)、(353,347)、(354,346)、(355,345)共11个,…(10分)
事件A包含的基本事件有:(351,349)、(352,348)、(353,347)、(354,346)、(355,345)共5个.
∴P(A)=
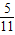 .…(13分)
.…(13分)点评:本题主要考查了抽样方法中的分层抽样,以及古典概型的概率,同时考查了运算求解的能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(13分) 某高级中学共有学生3 000名,各年级男、女生人数如下表:
| 高一年级 | 高二年级 | 高三年级 | |
| 男生 | 595 | 560 | y |
| 女生 | 605 | x | z |
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.18.
(1)求x的值;
(2)现用分层抽样的方法在全校抽取120名学生,问应在高三年级抽取学生多少名?
(3)在(2)的前提下,已知y≥345,z≥345,求高三年级中男生比女生多的概率.
某高级中学共有学生3 000名,各年级男、女生人数如下表:
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.18.
(1)求x的值;
(2)现用分层抽样的方法在全校抽取120名学生,问应在高三年级抽取学生多少名?
(3)在(2)的前提下,已知y≥345,z≥345,求高三年级中男生比女生多的概率.
| 高一年级 | 高二年级 | 高三年级 | |
| 男生 | 595 | 560 | y |
| 女生 | 605 | x | z |
(1)求x的值;
(2)现用分层抽样的方法在全校抽取120名学生,问应在高三年级抽取学生多少名?
(3)在(2)的前提下,已知y≥345,z≥345,求高三年级中男生比女生多的概率.