题目内容
在三棱锥S-ABC中,E,F中分别为棱SC,AB的中点,若AC=SB=2,EF=
,则异面直线AC和SB所成的角为( )
| 2 |
分析:取SA的中点D,连结DE、DF,根据三角形中位线定理证出DE∥AC且DF∥SB,DE=DF=1,可得∠EDF(或其补角)就是异面直线AC和SB所成的角.再根据题中数据,利用余弦定理在△DEF中算出∠EDF的大小,从而得到答案.
解答:解: 取SA的中点D,连结DE、DF,
取SA的中点D,连结DE、DF,
∵△SAC中,DE是中位线,
∴DE∥AC,DE=
AC=1.
同理DF∥SB,DF=
SB=1.
因此,∠EDF(或其补角)就是异面直线AC和SB所成的角.
∵△DEF中,DE=DF=1,EF=
,
∴DE2+DF2=2=EF2,
可得cos∠EDF=
=0,∠EDF=90°.
即异面直线AC和SB所成的角为90°.
故选:C
 取SA的中点D,连结DE、DF,
取SA的中点D,连结DE、DF,∵△SAC中,DE是中位线,
∴DE∥AC,DE=
| 1 |
| 2 |
同理DF∥SB,DF=
| 1 |
| 2 |
因此,∠EDF(或其补角)就是异面直线AC和SB所成的角.
∵△DEF中,DE=DF=1,EF=
| 2 |
∴DE2+DF2=2=EF2,
可得cos∠EDF=
| DE2+DF2-EF2 |
| 2DE•DF |
即异面直线AC和SB所成的角为90°.
故选:C
点评:本题给出三棱锥满足的条件,求异面直线所成角的大小,着重考查了三角形中位线定理、余弦定理和异面直线的定义及求法等知识,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.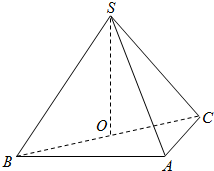 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点. 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2, C.
C. 如图,在三棱锥S-ABC中,
如图,在三棱锥S-ABC中,