题目内容
已知椭圆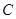 的中心为坐标原点
的中心为坐标原点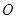 ,一个长轴端点为
,一个长轴端点为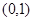 ,短轴端点和焦点所组成的四边形为正方形,若直线
,短轴端点和焦点所组成的四边形为正方形,若直线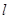 与
与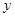 轴交于点
轴交于点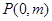 ,与椭圆
,与椭圆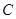 交于不同的两点
交于不同的两点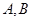 ,且
,且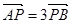 。(14分)
。(14分)
(1)求椭圆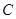 的方程;
的方程;
(2)求实数 的取值范围。
的取值范围。
【答案】
(1)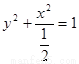 (2)-1<m<
(2)-1<m<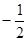 或
或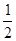 <m<1
<m<1
【解析】
试题分析:(1)∵一个长轴端点为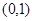 ,所以
,所以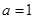 ,且焦点在y轴上,
,且焦点在y轴上,
因为短轴端点和焦点所组成的四边形为正方形,所以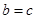 ,
,
又因为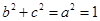 ,所以
,所以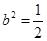 ,所以椭圆方程为
,所以椭圆方程为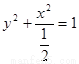 .
.
(2)(1)当直线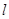 斜率不存在时,不符题意,斜率为0时显然也不符题意;
斜率不存在时,不符题意,斜率为0时显然也不符题意;
设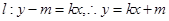 ,
,
由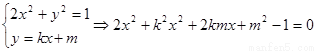 ,
,
∴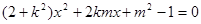 ,
,
设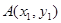 ,
,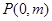 ,
,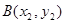 ,
,
所以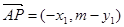 ,
,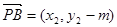 ,
,
所以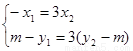 ,所以
,所以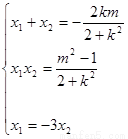 , 消去
, 消去 得
得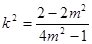 ,
,
又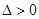 ,∴
,∴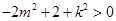 ,
,
∴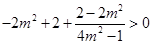 , ∴
, ∴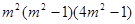 <0, ∴-1<m<
<0, ∴-1<m<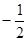 或
或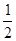 <m<1.
<m<1.
考点:本小题主要考查直线与圆锥曲线的位置关系.
点评:求解直线与圆锥曲线的位置关系时,免不了要联立直线方程和圆锥曲线方程,此时一般运算量比较大,综合考查学生分析问题、解决问题的能力和运算求解能力.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目