题目内容
给出下列四个命题:命题p1:“a=0,b≠0”是“函数y=x2+ax+b为偶函数”的必要不充分条件;命题p2:函数 是奇函数,则下列命题是真命题的是( )
是奇函数,则下列命题是真命题的是( )A.p1∧p2
B.p1∨¬p2
C.p1∨p2
D.p1∧¬p2
【答案】分析:由偶函数的定义f(-x)=f(x),可判断命题p1的真假;由奇函数的定义f(-x)=f(x),及对数函数的性质可判断命题p2的真假;最后由复合命题的真假关系,即可得出判断.
解答:解:①“a=0,b≠0”⇒“函数y=x2+ax+b=x2+b为偶函数”;
“函数y=x2+ax+b为偶函数”⇒“x2+ax+b=(-x)2-ax+b”⇒“a=0”.显然可以b=0.
所以“a=0,b≠0”是“函数y=x2+ax+b为偶函数”的充分不必要条件.
所以命题p1是假命题.
②函数f(x)=ln 的定义域是(-1,1),且f(-x)=ln
的定义域是(-1,1),且f(-x)=ln =-ln
=-ln =-f(x),所以该函数是奇函数.
=-f(x),所以该函数是奇函数.
所以命题p2是真命题.
综合①②知p1∨p2是真命题.
故选C.
点评:奇偶性是函数的重要性质,注意形如y=loga (a>0,且a≠1,b≠0)的函数是奇函数;复合命题p且q的真假关系可记为:一假即假,复合命题p或q的真假关系可记为:一真即真.
(a>0,且a≠1,b≠0)的函数是奇函数;复合命题p且q的真假关系可记为:一假即假,复合命题p或q的真假关系可记为:一真即真.
解答:解:①“a=0,b≠0”⇒“函数y=x2+ax+b=x2+b为偶函数”;
“函数y=x2+ax+b为偶函数”⇒“x2+ax+b=(-x)2-ax+b”⇒“a=0”.显然可以b=0.
所以“a=0,b≠0”是“函数y=x2+ax+b为偶函数”的充分不必要条件.
所以命题p1是假命题.
②函数f(x)=ln
 的定义域是(-1,1),且f(-x)=ln
的定义域是(-1,1),且f(-x)=ln =-ln
=-ln =-f(x),所以该函数是奇函数.
=-f(x),所以该函数是奇函数.所以命题p2是真命题.
综合①②知p1∨p2是真命题.
故选C.
点评:奇偶性是函数的重要性质,注意形如y=loga
 (a>0,且a≠1,b≠0)的函数是奇函数;复合命题p且q的真假关系可记为:一假即假,复合命题p或q的真假关系可记为:一真即真.
(a>0,且a≠1,b≠0)的函数是奇函数;复合命题p且q的真假关系可记为:一假即假,复合命题p或q的真假关系可记为:一真即真. 
练习册系列答案
相关题目
 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题: ,
, ,则
,则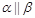 ;
; ,
, ,
, ,
, ,则
,则 ;
;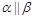 ,
, ,则
,则 ;
; ,
, ,
, ,
, ,则
,则 其中真命
其中真命