题目内容
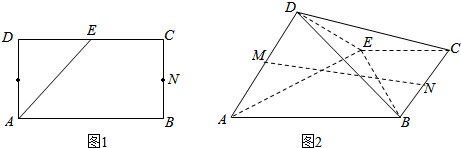
16.如图1,矩形ABCD,AB=2BC=4,M,N,E分别为AD,BC,CD的中点.现将△ADE沿AE折起,折起过程中,点D仍记作D,得到如图2所示的四棱锥D-ABCE.(1)证明:MN∥平面CDE;
(2)当AD⊥BE时,求直线BD与平面CDE所成角的正弦值.
分析 (1)取BD中点O,连结MO,NO,由已知推导出NO∥CE,MO∥CE,由此能证明平面CDE∥平面MNO,从而MN∥平面CDE.
(2)以E为原点,EA为x轴,EB为y轴,建立空间直角坐标系,利用向量法能求出直线BD与平面CDE所成角的正弦值.
解答  证明:(1)取BD中点O,连结MO,NO,
证明:(1)取BD中点O,连结MO,NO,
∵M,N分别为AD,BC的中点,∴NO∥CE,MO∥AB,
∵CE∥AB,∴MO∥CE,
∵MO∩NO=O,CE∩CD=C,
∴平面CDE∥平面MNO,
∵MN?平面MNO,∴MN∥平面CDE.
解:(2)∵AB=2BC=4,E是CD中点,∴AE=BE=$\sqrt{4+4}$=2$\sqrt{2}$,
∴AE2+BE2=AB2,∴AE⊥BE,
以E为原点,EA为x轴,EB为y轴,建立如图所示的空间直角坐标系,
C(-2,$\sqrt{2}$,0),A(2$\sqrt{2}$,0,0),B(0,2$\sqrt{2}$,0),
设D(a,b,c),则$\overrightarrow{AD}$=(a-2$\sqrt{2}$,b,c),$\overrightarrow{ED}$=(a,b,c),$\overrightarrow{BD}$=(a,b-2$\sqrt{2}$,c),$\overrightarrow{EB}$=(0,2$\sqrt{2}$,0),
∵AD⊥BE,AD⊥DE,BE∩DE=E,∴AD⊥平面BDE,
∴$\overrightarrow{AD}•\overrightarrow{EB}$=2$\sqrt{2}b$=0,∴D(a,o,c),
∵AD=DE=2,AE=2$\sqrt{2}$,∴a=c=$\sqrt{2}$,∴D($\sqrt{2},0,\sqrt{2}$),
∴$\overrightarrow{BD}$=($\sqrt{2}$,-2$\sqrt{2}$,$\sqrt{2}$),$\overrightarrow{EC}$=(-2,$\sqrt{2}$,0),$\overrightarrow{ED}$=($\sqrt{2},0,\sqrt{2}$),
设平面CDE的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EC}=-2x+\sqrt{2}y=0}\\{\overrightarrow{n}•\overrightarrow{ED}=\sqrt{2}x+\sqrt{2}z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,$\sqrt{2}$,-1),
设直线BD与平面CDE所成角为θ,
则sinθ=$\frac{|\overrightarrow{BD}•\overrightarrow{n}|}{|\overrightarrow{BD}|•|\overrightarrow{n}|}$=$\frac{|-4|}{\sqrt{12}•2}$=$\frac{\sqrt{3}}{3}$.
∴直线BD与平面CDE所成角的正弦值为$\frac{\sqrt{3}}{3}$.
点评 本题考查线面平行的证明,考查线面角的正弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 名校课堂系列答案
名校课堂系列答案| A. | 1:9 | B. | 1:27 | C. | 1:3 | D. | 1:3$\sqrt{3}$ |
| A. | 2 | B. | 2或$-\frac{1}{2}$ | C. | -2 | D. | $\frac{3}{4}$ |
| A. | [0,1] | B. | [-1,0] | C. | [1,+∞) | D. | (-∞,1] |
| A. | (-5,1) | B. | (-∞,-5)∪(1,+∞) | C. | (-1,5) | D. | (-∞,-1)∪(5,+∞) |