题目内容
若
(sinx-acosx)dx=2,则实数a等于
| ∫ |
0 |
-1
-1
.分析:根据定积分计算公式,算出
(sinx-acosx)dx=-a+1,再结合本题的等式解关于a的方程,即可得到实数a的值.
| ∫ |
0 |
解答:解:
(sinx-acosx)dx=(-cosx-asinx)
=[(-cos
-asin
)-(-cos0-asin0)]=-a+1
∵
(sinx-acosx)dx=2
∴-a+1=2,解之得a=-1
故答案为:-1
| ∫ |
0 |
| | |
0 |
| π |
| 2 |
| π |
| 2 |
∵
| ∫ |
0 |
∴-a+1=2,解之得a=-1
故答案为:-1
点评:本题给出含有字母参数a的积分方程,叫我们解出实数a的值,着重考查了定积分计算公式和运算法则等知识,属于基础题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
若
(sinx-acosx)dx=2,则实数a等于( )
| ∫ |
0 |
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
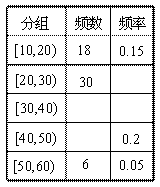 得到的样本的频率分布直方图如图所示.
得到的样本的频率分布直方图如图所示. 的展开式中的常数项是20;
的展开式中的常数项是20;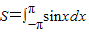 ;
;