题目内容
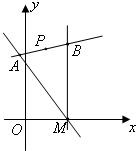 如图,过点P(1,5)作直线l,与直线a:y=-
如图,过点P(1,5)作直线l,与直线a:y=-| 3 |
| 3 |
分析:易得M(2,0),当AB平行于x轴时,A(2-
,5)、B(2,5),|AB|=
,S△ABM为
,当AB斜率存在,设直线AB的方程为 y-5=k (x-1),将AB的方程分别与直线a、直线b的方程联立,可得A,B坐标,再求|AB|弦长和点M到直线AB的距离,由三角形面积公求解.
5
| ||
| 3 |
5
| ||
| 3 |
25
| ||
| 6 |
解答:解:易得M(2,0),当AB平行于x轴时,A(2-
,5)、B(2,5),|AB|=
S△ABM为
,
由题意知,AB斜率存在,设AB斜率为k,则直线AB的方程为 y-5=k (x-1),
将 AB的方程分别与直线a、直线b的方程联立,可得A(
,
),B(2,k+5),
|AB|=
,点M到直线AB的距离为:d=
S△ABM=
|AB|•d=
≥10-2
5
| ||
| 3 |
5
| ||
| 3 |
25
| ||
| 6 |
由题意知,AB斜率存在,设AB斜率为k,则直线AB的方程为 y-5=k (x-1),
将 AB的方程分别与直线a、直线b的方程联立,可得A(
k+2
| ||
k+
|
| ||||
k+
|
|AB|=
|5+K|
| ||
k+
|
| |7-k| | ||
|
S△ABM=
| 1 |
| 2 |
| k2-k+35 | ||
k+
|
| 3 |
点评:本题主要考查用几何法几三角形的面积,涉及到弦长公式,点到直线的距离等问题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
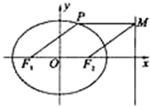 如图,点P在椭圆
如图,点P在椭圆 如图,点P在椭圆
如图,点P在椭圆 如图,过点P(1,5)作直线l,与直线
如图,过点P(1,5)作直线l,与直线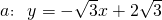 、直线b:x=2分别交于A、B两点,M为直线a与直线b的交点,则△ABM面积的最小值为 ________.
、直线b:x=2分别交于A、B两点,M为直线a与直线b的交点,则△ABM面积的最小值为 ________. 、直线b:x=2分别交于A、B两点,M为直线a与直线b的交点,则△ABM面积的最小值为 .
、直线b:x=2分别交于A、B两点,M为直线a与直线b的交点,则△ABM面积的最小值为 .