题目内容
已知函数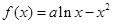 .
.
(1)当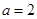 时,求函数
时,求函数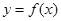 在
在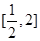 上的最大值;
上的最大值;
(2)令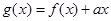 ,若
,若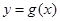 在区间
在区间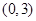 上不单调,求
上不单调,求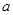 的取值范围;
的取值范围;
(3)当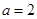 时,函数
时,函数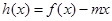 的图象与
的图象与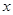 轴交于两点
轴交于两点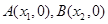 ,且
,且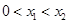 ,又
,又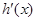 是
是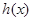 的导函数.若正常数
的导函数.若正常数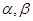 满足条件
满足条件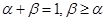 .证明:
.证明: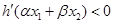 .
.
(1)-1;(2)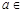
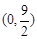 ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(1)根据利用导数求函数在闭区间上的最值的方法即可求得.
(2)首先将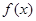 代入得
代入得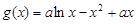 ,然后求导:
,然后求导: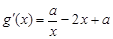 .
.
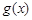 在区间
在区间 上不单调,那么方程
上不单调,那么方程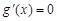 在(0,3)上应有实数解,且不是重根即解两侧的导数值小于0.
在(0,3)上应有实数解,且不是重根即解两侧的导数值小于0.
将方程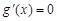 变形分离变量得:
变形分离变量得: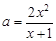
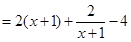 .下面就研究函数
.下面就研究函数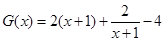 ,易得函数
,易得函数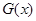 在
在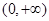 上单调递增,所以
上单调递增,所以 ,(
,(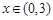 ).结合图象知,
).结合图象知,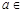
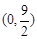 时,
时,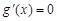 在(0,3)上有实数解.这些解会不会是重根呢?
在(0,3)上有实数解.这些解会不会是重根呢?
由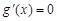 得:
得: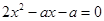 ,若有重根,则
,若有重根,则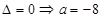 或
或 .这说明
.这说明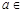
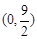 时,没有重根. 由此得:
时,没有重根. 由此得: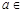
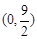 .
.
(3)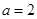 时,
时,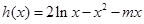 ,所以
,所以 .
. 有两个实根
有两个实根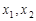 ,则将两根代入方程,可得
,则将两根代入方程,可得 .
.
再看看待证不等式: ,这里面不仅有
,这里面不仅有 ,还有
,还有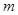 ,那么是否可以消去一些字母呢?
,那么是否可以消去一些字母呢?
将 两式相减,得
两式相减,得 ,
变形得:
,
变形得:
 , 将此式代入上面不等式即可消去
, 将此式代入上面不等式即可消去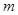 ,整理可得:
,整理可得:
 ,再变形得:
,再变形得: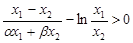 .下面就证这个不等式.这类不等式就很常见了,一般是将
.下面就证这个不等式.这类不等式就很常见了,一般是将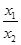 看作一个整体,令
看作一个整体,令 ,又转化为
,又转化为 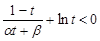 ,只需证
,只需证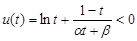 即可.而这利用导数很易得证.
即可.而这利用导数很易得证.
试题解析:(1) 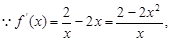
函数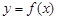 在[
在[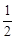 ,1]是增函数,在[1,2]是减函数,
3分
,1]是增函数,在[1,2]是减函数,
3分
所以 .
4分
.
4分
(2)因为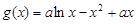 ,所以
,所以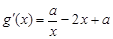 ,
5分
,
5分
因为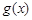 在区间
在区间 上不单调,所以
上不单调,所以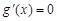 在(0,3)上有实数解,且无重根,
在(0,3)上有实数解,且无重根,
由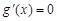 ,有
,有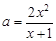 =
= ,(
,(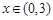 )
6分
)
6分
又当 时,
时,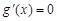 有重根
有重根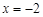 ;
; 时,
时,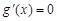 有重根
有重根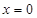 .
7分
.
7分
综上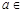
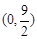 8分
8分
(3)∵ ,又
,又 有两个实根
有两个实根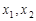 ,
,
∴ ,两式相减,得
,两式相减,得 ,
,
∴ ,
10分
,
10分
于是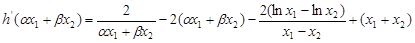
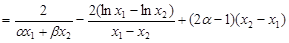 .
11分
.
11分
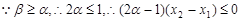 .
.
要证: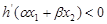 ,只需证:
,只需证:
只需证: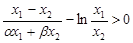 .(*)
12分
.(*)
12分
令 ,∴(*)化为
,∴(*)化为 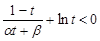 ,只证
,只证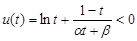 即可.
即可. 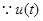 在(0,1)上单调递增,
在(0,1)上单调递增, ,即
,即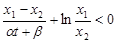 .∴
.∴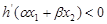 . 14分
. 14分
考点:1、导数的应用;2、不等式的证明.

 ,
,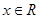 .
.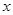 为何值时,
为何值时,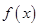 取得最大值,并求出其最大值;
取得最大值,并求出其最大值; ,
,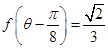 ,求
,求 的值.
的值.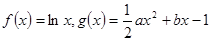 ,
, 且
且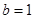 时,证明:对
时,证明:对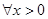 ,
,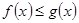 ;
;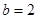 ,且
,且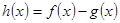 存在单调递减区间,求
存在单调递减区间,求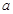 的取值范围;
的取值范围;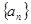 ,若存在常数
,若存在常数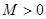 ,
,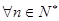 ,都有
,都有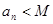 ,则称数列
,则称数列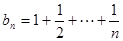 ,试判断数列
,试判断数列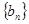 是否有上界.
是否有上界.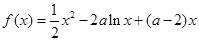 ,
,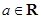 .
.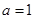 时,求函数
时,求函数 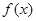 的最小值;
的最小值; 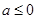 时,讨论函数
时,讨论函数 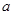 ,对任意的
,对任意的
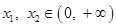 ,且
,且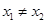 ,有
,有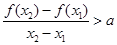 ,恒成立,若存在求出
,恒成立,若存在求出