题目内容
已知函数![]() ,其中
,其中![]()
![]()
![]()
(1) 当![]() 满足什么条件时,
满足什么条件时,![]() 取得极值?
取得极值?
(2) 已知![]() ,且
,且![]() 在区间
在区间![]() 上单调递增,试用
上单调递增,试用![]() 表示出
表示出![]() 的取值范围.
的取值范围.
解析: (1)由已知得![]() ,令
,令![]() ,得
,得![]() ,
,
![]() 要取得极值,方程
要取得极值,方程![]() 必须有解,
必须有解,
所以△![]() ,即
,即![]() , 此时方程
, 此时方程![]() 的根为
的根为
![]() ,
,![]() ,
,
所以![]()
![]()
![]()
当![]() 时,
时,
x | (-∞,x1) | x 1 | (x1,x2) | x2 | (x2,+∞) |
f’(x) | + | 0 | - | 0 | + |
f (x) | 增函数 | 极大值 | 减函数 | 极小值 | 增函数 |
所以![]() 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
当![]() 时,
时, ![]()
x | (-∞,x2) | x 2 | (x2,x1) | x1 | (x1,+∞) |
f’(x) | - | 0 | + | 0 | - |
f (x) | 减函数 | 极小值 | 增函数 | 极大值 | 减函数 |
所以![]() 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
综上,当![]() 满足
满足![]() 时,
时, ![]() 取得极值.
取得极值. ![]()
![]()
(2)要使![]() 在区间
在区间![]() 上单调递增,需使
上单调递增,需使![]() 在
在![]() 上恒成立.
上恒成立.
即![]() 恒成立, 所以
恒成立, 所以![]()
设![]() ,
,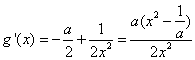 ,
,
令![]() 得
得![]() 或
或![]() (舍去),
(舍去),![]()
![]()
当![]() 时,
时,![]() ,当
,当![]() 时
时![]() ,
,![]() 单调增函数;
单调增函数;
当![]() 时
时![]() ,
,![]() 单调减函数,
单调减函数,
所以当![]() 时,
时,![]() 取得最大,最大值为
取得最大,最大值为![]() .
.
所以![]()
当![]() 时,
时,![]() ,此时
,此时![]() 在区间
在区间![]() 恒成立,所以
恒成立,所以![]() 在区间
在区间![]() 上单调递增,当
上单调递增,当![]() 时
时![]() 最大,最大值为
最大,最大值为![]() ,所以
,所以![]()
综上,当![]() 时,
时, ![]() ; 当
; 当![]() 时,
时, ![]()
![]()
![]()
【命题立意】:本题为三次函数,利用求导的方法研究函数的极值、单调性和函数的最值,函数在区间上为单调函数,则导函数在该区间上的符号确定,从而转为不等式恒成立,再转为函数研究最值.运用函数与方程的思想,化归思想和分类讨论的思想解答问题.

练习册系列答案
相关题目

 其中
其中 (其中常数a,b∈R)。
(其中常数a,b∈R)。  是奇函数.
是奇函数. 的表达式;
的表达式; 在区间[1,2]上的最大值和最小值.
在区间[1,2]上的最大值和最小值. 其中a>0,e为自然对数的底数。
其中a>0,e为自然对数的底数。
 的单调区间;
的单调区间;