题目内容
焦点在 x轴上,虚轴长为12,离心率为
的双曲线标准方程是( )
| 5 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:由虚轴长是12求出半虚轴b,根据双曲线的性质c2=a2+b2以及离心率然,求出a2,写出双曲线的标准方程.
解答:解:根据题意可知2b=12,解得b=6 ①
又因为离心率e=
=
②
根据双曲线的性质可得a2=c2-b2 ③
由①②③得,a2=64
双所以满足题意的双曲线的标准方程为:
-
=1
故选D
又因为离心率e=
| c |
| a |
| 5 |
| 4 |
根据双曲线的性质可得a2=c2-b2 ③
由①②③得,a2=64
双所以满足题意的双曲线的标准方程为:
| x2 |
| 64 |
| y2 |
| 36 |
故选D
点评:此题考查学生掌握双曲线的性质,会利用待定系数法求双曲线的标准方程,是一道中档题.

练习册系列答案
相关题目
 ;
;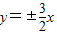 .
. ;
;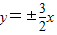 .
.