题目内容
设二次函数 的图象在点
的图象在点 的切线方程为
的切线方程为 ,若
,若
则下面说法正确的有: .
①存在相异的实数 使
使 成立;
成立;
② 在
在 处取得极小值;
处取得极小值;
③ 在
在 处取得极大值;
处取得极大值;
④不等式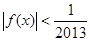 的解集非空;
的解集非空;
⑤直线 一定为函数
一定为函数 图像的对称轴.
图像的对称轴.
【答案】
①④⑤
【解析】
试题分析:设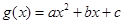 ,则
,则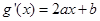 ,所以
,所以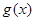 在点
在点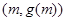 处的切线方程为
处的切线方程为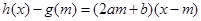 ,即
,即 ,所以
,所以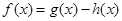
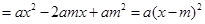 ,这是二次函数,则①正确;当
,这是二次函数,则①正确;当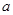 的正负不确定,故
的正负不确定,故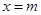 不能确定其为极大值还是极小值,所以②③不正确;而当
不能确定其为极大值还是极小值,所以②③不正确;而当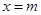 时,
时, ,所以其解集非空,④正确;易知
,所以其解集非空,④正确;易知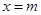 一定是
一定是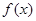 图像的对称轴.故①④⑤正确.
图像的对称轴.故①④⑤正确.
考点:1.二次函数的性质;2.函数的切线方程求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图象过点
的图象过点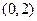 ,其导函数为
,其导函数为 ,数列
,数列
 项和为
项和为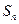 ,点
,点 在函数
在函数 .
. 的解析式;
的解析式; ,求数列
,求数列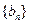 的前
的前 .
. 的图象在点
的图象在点 的切线方程为
的切线方程为 ,若
,若
 使
使 成立;
成立;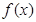 在
在 处取得极小值;
处取得极小值; 的解集非空;
的解集非空;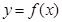 的图象过点
的图象过点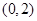 ,其导函数为
,其导函数为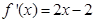 ,数列
,数列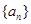
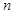 项和为
项和为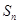 ,点
,点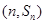 在函数
在函数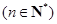 .
.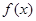 的解析式;
的解析式;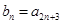 ,求数列
,求数列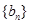 的前
的前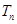 .
. 的图象以
的图象以 轴为对称轴,已知
轴为对称轴,已知 ,而且若点
,而且若点 在
在 的图象上,则点
的图象上,则点 在函数
在函数 的图象上
的图象上 的解析式
的解析式 ,问是否存在实数
,问是否存在实数 ,使
,使 在
在 内是减函数,在
内是减函数,在 内是增函数。
内是增函数。