题目内容
对于区间[m,n]上有意义的两个函数f(x)与g(x),如果任意x∈[m,n],均有|f(x)-g(x)|≤1,则称f(x)与g(x)在[m,n]上是接近的,否则称f(x)与g(x)在[m,n]上是非接近的.现有两个函数f1(x)=loga(x-3a)与f2(x)=loga (a>0,a≠1)
(a>0,a≠1)(1)求f1(x)-f2(x)的定义域;
(2)若f1(x)与f2(x)在整个给定区间[a+2,a+3]上都有意义,
①求a的取值范围;
②讨论f1(x)与f2(x)在整个给定区间[a+2,a+3]上是不是接近的.
【答案】分析:(1)利用求函数定义域的方法求函数的定义域.
(2)利用函数的新定义确定a的取值范围.
解答:解:(1)因为f1(x)-f2(x)=loga(x-3a)-loga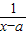 (a>0,a≠1),
(a>0,a≠1),
所以要使函数有意义,则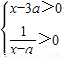 ,即
,即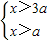 ,所以x>3a.
,所以x>3a.
定义域为(3a,+∞)…(1分)
(2)①由3a<a+2∴0<a<1…(2分)
②若f1(x)与f2(x)在[a+2,a+3]上接近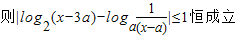
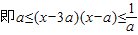 …(4分)
…(4分)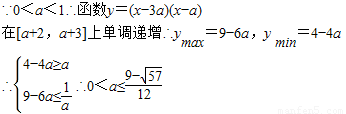
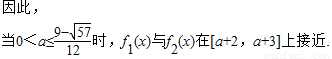
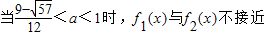 .…(8分)
.…(8分)
点评:本题主要考查对数函数的性质和应用,考查学生分析问题的能力,综合性较强,运算量较大.
(2)利用函数的新定义确定a的取值范围.
解答:解:(1)因为f1(x)-f2(x)=loga(x-3a)-loga
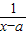 (a>0,a≠1),
(a>0,a≠1),所以要使函数有意义,则
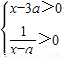 ,即
,即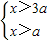 ,所以x>3a.
,所以x>3a.定义域为(3a,+∞)…(1分)
(2)①由3a<a+2∴0<a<1…(2分)
②若f1(x)与f2(x)在[a+2,a+3]上接近
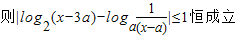
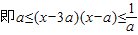 …(4分)
…(4分)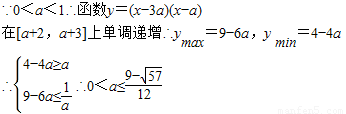
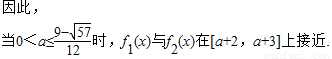
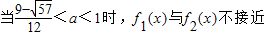 .…(8分)
.…(8分)点评:本题主要考查对数函数的性质和应用,考查学生分析问题的能力,综合性较强,运算量较大.

练习册系列答案
相关题目
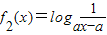 (a>0且a≠1),f1(x)与f2(x)在给定区间[a+2,a+3]上都有意义,
(a>0且a≠1),f1(x)与f2(x)在给定区间[a+2,a+3]上都有意义,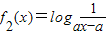 (a>0且a≠1),f1(x)与f2(x)在给定区间[a+2,a+3]上都有意义,
(a>0且a≠1),f1(x)与f2(x)在给定区间[a+2,a+3]上都有意义,