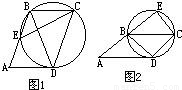
题目内容
过平行四边形ABCD的顶点B、C、D的圆与直线AD相切,与直线AB相交于点E,已知AD=4,CE=5.(1)如图1,若点E在线段AB上,求AE的长;
(2)点E能否在线段AB的延长线上?(即图2的情形是否存在?)若能,求出AE的长;若不能,请说明理由.
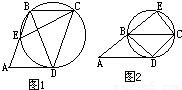
【答案】分析:(1)由圆的内接梯形得线段相等,再利用切割线定理解决第(1)题,
(2)而第(2)题是探究性问题,利用反证法证明,应假设其存在,再推出矛盾或符合题意.
解答:解:(1)由圆的内接梯形知BD=EC=5,
由同弧上的圆周角和弦切角的关系可得
△DCE为等腰三角形,且AB=CD=CE=BD,
再由切割线定理得:AD2=AB•AE,
∵AD=4,AB=CE=5,
∴得AE=3.2;
(2)点E不能在AB的延长线上.
假设图形(2)存在,
则由已知得AB=BD=CE,
又AD2=AB•AE=CE•AE≥CE2,
∴CE2≤16,
即CE≤4与已知矛盾.
故假设不存在,
点E不能在AB的延长线上.
点评:本题主要考查了反证法、圆的切割线定理等,对于探究性问题,常利用反证法进行证明,首先应假设其存在,再推出矛盾或符合题意.
(2)而第(2)题是探究性问题,利用反证法证明,应假设其存在,再推出矛盾或符合题意.
解答:解:(1)由圆的内接梯形知BD=EC=5,
由同弧上的圆周角和弦切角的关系可得
△DCE为等腰三角形,且AB=CD=CE=BD,
再由切割线定理得:AD2=AB•AE,
∵AD=4,AB=CE=5,
∴得AE=3.2;
(2)点E不能在AB的延长线上.
假设图形(2)存在,
则由已知得AB=BD=CE,
又AD2=AB•AE=CE•AE≥CE2,
∴CE2≤16,
即CE≤4与已知矛盾.
故假设不存在,
点E不能在AB的延长线上.
点评:本题主要考查了反证法、圆的切割线定理等,对于探究性问题,常利用反证法进行证明,首先应假设其存在,再推出矛盾或符合题意.

练习册系列答案
相关题目
 21、过平行四边形ABCD的顶点B、C、D的圆与直线AD相切,与直线AB相交于点E,已知AD=4,CE=5.
21、过平行四边形ABCD的顶点B、C、D的圆与直线AD相切,与直线AB相交于点E,已知AD=4,CE=5.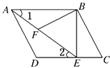 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.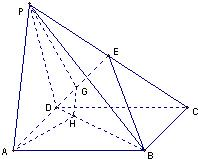 17、如图,点P为平行四边形ABCD所在平面外一点,点E为PC的中点,在DE上取一点G,过点G和直线AP作平面APG交平面BDE于GH,求证:AP∥GH.
17、如图,点P为平行四边形ABCD所在平面外一点,点E为PC的中点,在DE上取一点G,过点G和直线AP作平面APG交平面BDE于GH,求证:AP∥GH.