题目内容
函数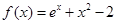 在区间
在区间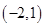 内零点的个数为 .
内零点的个数为 .
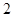 .
.
解析试题分析:因为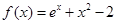 ,所以
,所以 ,
,
从而 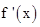 是增函数,且f'(-2)=
是增函数,且f'(-2)=  -4<0,f'(0)=1>0
-4<0,f'(0)=1>0
从而 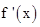 在(-2,1)内有唯一零点,设为
在(-2,1)内有唯一零点,设为 ,且-2<
,且-2< <0
<0
则在区间(-2, )上,有f'(x)<0,f(x)是减函数,
)上,有f'(x)<0,f(x)是减函数,
在区间( ,1)上,f'(x)>0,f(x)是增函数.
,1)上,f'(x)>0,f(x)是增函数.
因为f(-2)=  +2>0,f(
+2>0,f( )<f(0)=-1<0,f(1)=e-1>0
)<f(0)=-1<0,f(1)=e-1>0
从而 f(x)在(-2,1)上有两个零点.
考点:本题主要考查函数零点的概念,导数的计算。
点评:中档题,本解法利用了导数知识,通过研究函数的单调性,认识函数零点的个数。利用零点存在性定理,进行猜测行动计算或结合函数图象,也可以使问题得解。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
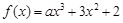 且
且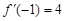 ,则实数
,则实数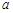 的值等于 ;
的值等于 ; 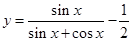 在点M(
在点M(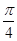 ,0)处的切线的斜率为________________.
,0)处的切线的斜率为________________.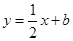 是曲线
是曲线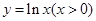 的一条切线,则实数
的一条切线,则实数 的值为
的值为 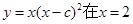 处有极大值,则常数c= ;
处有极大值,则常数c= ;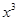 -x+3在点(1,3)处的切线方程为
-x+3在点(1,3)处的切线方程为 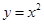 与函数
与函数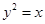 的图象围成的封闭图形的面积为
的图象围成的封闭图形的面积为 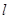 ,则f(2)+f'(2)=
,则f(2)+f'(2)= 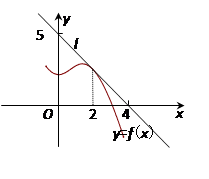
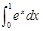 ,n=
,n=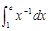 ,则m与n的大小关系为______.
,则m与n的大小关系为______.