题目内容
在直角坐标系内,△ABC的两个顶点C、A的坐标分别为(-
,0),(
,0),三个内角A、B、C满足2sinB=
(sinA+sinC).
(1)求顶点B的轨迹方程;
(2)过点C做倾斜角为θ的直线与顶点B的轨迹交于P、Q两点,当θ∈(0,
)时,求△APQ面积的最大值.
| 3 |
| 3 |
| 3 |
(1)求顶点B的轨迹方程;
(2)过点C做倾斜角为θ的直线与顶点B的轨迹交于P、Q两点,当θ∈(0,
| π |
| 2 |
分析:(1)由2sinB=
(sinA+sinC),根据正弦定理得2b=
(a+c),结合b=2
,可得a+c=4由椭圆定义知顶点B的轨迹为椭圆,可求
(2)设PQ方程为y=tanθ(x+
)联立直线与椭圆方程,设P(x1,y1),Q(x2,y2),根据方程的根与系数关系可求得x1+x1,x1x2,然后可求|PQ|及点A到PQ的距离d,代入可求△ABC的面积,由基本不等式可求最大值
| 3 |
| 3 |
| 3 |
(2)设PQ方程为y=tanθ(x+
| 3 |
解答: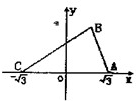 解:(1)因为2sinB=
解:(1)因为2sinB=
(sinA+sinC),根据正弦定理得2b=
(a+c)
又b=2
,所以a+c=4由椭圆定义知顶点B的轨迹为椭圆,其方程为
+y2=1(y≠0)
(2)设PQ方程为y=tanθ(x+
),θ∈(0,
)
由
得(1+4tan2θ)x2+8
xtan2θ+12tan2θ-4=0
设P(x1,y1),Q(x2,y2),则x1+x2=
,x1•x2=
,
又|PQ|=
,点A到PQ的距离d=
,θ∈(0,
)
S△ABC=
=
=
≤2
当且仅当
=3sinθ,即θ=arcsin
时取等号,△APQ的最大面积为2.
 解:(1)因为2sinB=
解:(1)因为2sinB=| 3 |
| 3 |
又b=2
| 3 |
| x2 |
| 4 |
(2)设PQ方程为y=tanθ(x+
| 3 |
| π |
| 2 |
由
|
| 3 |
设P(x1,y1),Q(x2,y2),则x1+x2=
-8
| ||
| 1+4tan2θ |
| 12tan2θ-4 |
| 1+4tan2θ |
又|PQ|=
| 4(1+tan2θ) |
| 1+4tan2θ |
|2
| ||
|
| π |
| 2 |
S△ABC=
4
| ||
| 1+4tan2θ |
4
| ||
| 1+3sin2θ |
4
| ||
|
当且仅当
| 1 |
| sinθ |
| ||
| 3 |
点评:本题主要考查了由三角形的正弦定理求解点的轨迹方程,直线与曲线相交关系的应用,方程的根与系数关系的应用,属于综合试题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目