题目内容
10.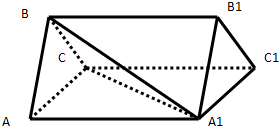 如图三棱柱ABC-A1B1C1中,底面ABC⊥侧面AA1C1C,△AA1C是正三角形,AB⊥BC且AB=BC.又三棱锥A-A1BC的体积是$\frac{9\sqrt{3}}{8}$.
如图三棱柱ABC-A1B1C1中,底面ABC⊥侧面AA1C1C,△AA1C是正三角形,AB⊥BC且AB=BC.又三棱锥A-A1BC的体积是$\frac{9\sqrt{3}}{8}$.(1)证明:AC⊥A1B;
(2)求直线BC和面ABA1所成角的正弦.
分析 (1)取AC的中点O,证明AC⊥平面A1BO,即可证明AC⊥A1B;
(2)求出AC,建立坐标系,求出面ABA1法向量,利用向量的夹角公式,即可求直线BC和面ABA1所成角的正弦.
解答  (1)证明:取AC的中点O,
(1)证明:取AC的中点O,
∵AB=BC,
∴BO⊥AC…(1分)
又△AA1C是正三角形,
∴A1O⊥AC,BO∩A1O=O,…(2分)
∴AC⊥平面A1BO…(3分)
又A1B?平面A1BO,
∴AC⊥A1B…(4分)
(2)解:设AC=a,则
∵三棱锥A-A1BC的体积是$\frac{9\sqrt{3}}{8}$,
∴$\frac{1}{3}•\frac{\sqrt{3}}{4}{a}^{2}•\frac{1}{2}a$=$\frac{9\sqrt{3}}{8}$,
∴a=3…(6分)
建系如图,则A(0,-$\frac{3}{2}$,0),B(0,0,$\frac{3}{2}$),C(0,$\frac{3}{2}$,0),A1($\frac{3\sqrt{3}}{2}$,0,0),
∴$\overrightarrow{{A}_{1}C}$=(-$\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$,0),$\overrightarrow{AB}$=(0,$\frac{3}{2}$,$\frac{3}{2}$),$\overrightarrow{A{A}_{1}}$=($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$,0),$\overrightarrow{CB}$=(0,-$\frac{3}{2}$,$\frac{3}{2}$),…(8分)
设面ABA1法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\frac{3}{2}y+\frac{3}{2}z=0}\\{\frac{3\sqrt{3}}{2}x+\frac{3}{2}y=0}\end{array}\right.$
得:$\overrightarrow{n}$=($\frac{\sqrt{3}}{3}$,-1,1)…(10分)
设直线BC和面ABA1所成角为θ,则sinθ=$\frac{3}{\sqrt{\frac{7}{3}•\frac{3}{2}\sqrt{2}}}$=$\frac{\sqrt{42}}{7}$.…(12分)
点评 本题考查线面垂直的判定与性质,考查线面角,考查向量知识的运用,考查学生分析解决问题的能力,正确求出平面的法向量是关键.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案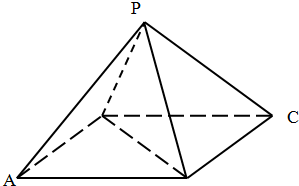 在四棱锥P-ABCD中,底面ABCD为菱形,且PA⊥BD,∠BAD=60°,AB=2
在四棱锥P-ABCD中,底面ABCD为菱形,且PA⊥BD,∠BAD=60°,AB=2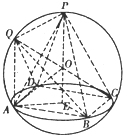 如图,正四棱锥P-ABCD的顶点都在同一球面上,已知ABCD中心为E,球心O在线段PE上,QA⊥底面ABCD,且与球面交于点Q,若球的半径为2.
如图,正四棱锥P-ABCD的顶点都在同一球面上,已知ABCD中心为E,球心O在线段PE上,QA⊥底面ABCD,且与球面交于点Q,若球的半径为2.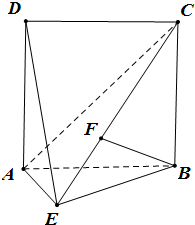 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.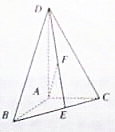 已知三棱椎D-ABC,AB=AC=1,AD=2,∠BAD=∠CAD=∠BAC=90°,点E,F分别是BC,DE的中点,如图所示,
已知三棱椎D-ABC,AB=AC=1,AD=2,∠BAD=∠CAD=∠BAC=90°,点E,F分别是BC,DE的中点,如图所示, 如图,P是平面ABCD外的一点,PA⊥平面ABCD,四边形ABCD是边长为2的正方形,PA=2,M、N分别为AD、BC的中点,MQ⊥PD于Q点.
如图,P是平面ABCD外的一点,PA⊥平面ABCD,四边形ABCD是边长为2的正方形,PA=2,M、N分别为AD、BC的中点,MQ⊥PD于Q点.