题目内容
已知集合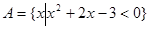 ,
,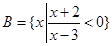 .
.
(1)在区间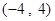 上任取一个实数
上任取一个实数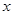 ,求“
,求“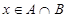 ”的概率;
”的概率;
(2)设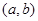 为有序实数对(如有序实数对(2,3)与(3,2)不一样),其中
为有序实数对(如有序实数对(2,3)与(3,2)不一样),其中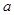 是从集合
是从集合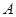 中任取的一个整数,
中任取的一个整数,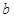 是从集合
是从集合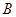 中任取的一个整数,求“
中任取的一个整数,求“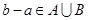 ”的概率
”的概率
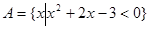 ,
,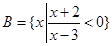 .
.(1)在区间
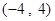 上任取一个实数
上任取一个实数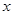 ,求“
,求“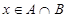 ”的概率;
”的概率;(2)设
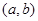 为有序实数对(如有序实数对(2,3)与(3,2)不一样),其中
为有序实数对(如有序实数对(2,3)与(3,2)不一样),其中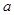 是从集合
是从集合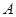 中任取的一个整数,
中任取的一个整数,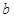 是从集合
是从集合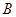 中任取的一个整数,求“
中任取的一个整数,求“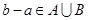 ”的概率
”的概率(Ⅰ)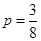 .(2)
.(2)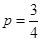 .
.
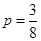 .(2)
.(2)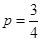 .
. 试题分析:(Ⅰ)易得
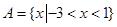 ,
,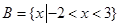 ,
,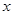 是区间
是区间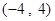 上的连续的实数,故属于几何概型,由几何概型的概率公式可得
上的连续的实数,故属于几何概型,由几何概型的概率公式可得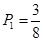 .(2)由于
.(2)由于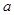 、
、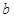 是整数,故属于古典概型,列出所有可能出现的结果,找出满足“
是整数,故属于古典概型,列出所有可能出现的结果,找出满足“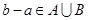 ”的所有结果,二者相除即得所求概率.
”的所有结果,二者相除即得所求概率.试题解析:(Ⅰ)∵
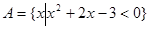 ∴
∴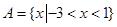 2分
2分∵
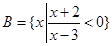 ∴
∴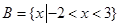 4分
4分设事件“
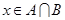 ”的概率为
”的概率为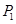 ,这是一个几何概型,则概率
,这是一个几何概型,则概率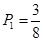 6分
6分(2)因为
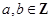 ,且
,且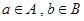 ,所以,基本事件共12个:
,所以,基本事件共12个: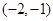 ,
,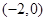 ,
,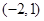 ,
,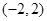 ,
,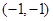 ,
,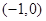 ,
,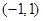 ,
,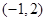 ,
,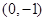 ,
,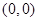 ,
,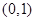 ,
,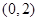 9分
9分设事件
 为“
为“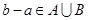 ”,则事件
”,则事件 中包含9个基本事件 11分
中包含9个基本事件 11分事件
 的概率
的概率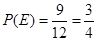 . 12分
. 12分
练习册系列答案
相关题目
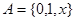 ,
,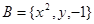 ,若
,若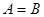 ,则
,则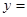 .
. ,
, ,且
,且 ,则A中的元素
,则A中的元素 对应集合B中的元素为( )
对应集合B中的元素为( )



 ,∴
,∴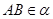 .
. ,∴
,∴ .
. ,∴
,∴ .
.  ,∴
,∴ .
.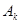 :(1)所有元素都是正整数;(2)最小元素为1;(3)最大元素为2014;(4)各个元素可以从小到大排成一个公差为
:(1)所有元素都是正整数;(2)最小元素为1;(3)最大元素为2014;(4)各个元素可以从小到大排成一个公差为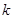
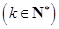 的等差数列.那么
的等差数列.那么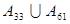 中元素的个数是( )
中元素的个数是( )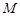 是
是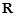 的子集,如果点
的子集,如果点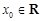 满足:
满足: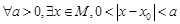 ,称
,称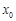 为集合
为集合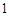 为聚点的有:
为聚点的有: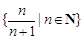 ; ②
; ②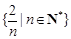 ;③
;③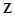 ;④
;④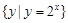 ( )
( )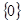 表示同一个集合
表示同一个集合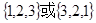
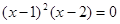 的所有解的集合可表示为
的所有解的集合可表示为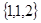
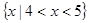 可以用列举法表示
可以用列举法表示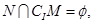 则
则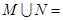 ( )
( )