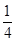题目内容
若过点(0,-1)作抛物线y=ax2(a>0)的两条切线互相垂直,则a为( )A.1
B.2
C.

D.

【答案】分析:由题意设出两条切线的方程,再与抛物线方程联立消去y后,得到关于x的二次方程,再由切线与曲线相切得判别式为零,列出两个方程求出a的值.
解答:解:由题意过点(0,-1)的切线的斜率存在,
设过点(0,-1)的两条切线的方程分别为:
y=kx-1和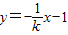 ,
,
由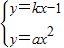 得,ax2-kx+1=0,
得,ax2-kx+1=0,
则△=k2-4a=0 ①,
同理可得,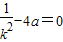 ②,
②,
由①②解得,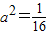 ,
,
∵a>0,∴a= ,
,
故选D.
点评:本题考查了切线与曲线位置关系,两直线垂直的充要条件,主要利用代数法:联立方程利用判别式的符号来解决.
解答:解:由题意过点(0,-1)的切线的斜率存在,
设过点(0,-1)的两条切线的方程分别为:
y=kx-1和
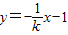 ,
,由
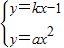 得,ax2-kx+1=0,
得,ax2-kx+1=0,则△=k2-4a=0 ①,
同理可得,
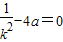 ②,
②,由①②解得,
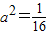 ,
,∵a>0,∴a=
 ,
,故选D.
点评:本题考查了切线与曲线位置关系,两直线垂直的充要条件,主要利用代数法:联立方程利用判别式的符号来解决.

练习册系列答案
相关题目
 的两条切线互相垂直,则a为( )
的两条切线互相垂直,则a为( )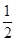 D.
D.