题目内容
(本题14分)如图,直线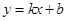 与椭圆
与椭圆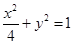 交于
交于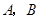 两点,记
两点,记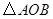 的面积为
的面积为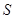 .
.
(I)求在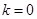 ,
,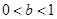 的条件下,
的条件下,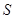 的最大值;
的最大值;
(II)当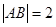 ,
,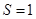 时,求直线
时,求直线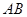 的方程.
的方程.

【答案】
(I)当且仅当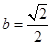 时,
时,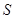 取到最大值
取到最大值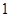 .
.
(II)直线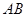 的方程是
的方程是
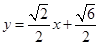 或
或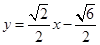 或
或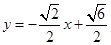 ,或
,或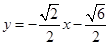 。
。
【解析】(Ⅰ)解:设点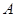 的坐标为
的坐标为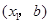 ,点
,点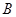 的坐标为
的坐标为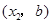 ,
,
由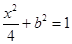 ,解得
,解得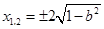 ,
,
所以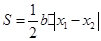
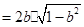
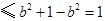 .
.
当且仅当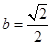 时,
时,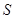 取到最大值
取到最大值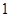 .
.
(Ⅱ)解:由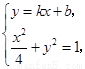
得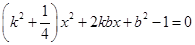 ,
,
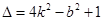 ,
,
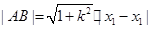
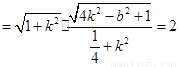 .
②
.
②
设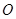 到
到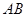 的距离为
的距离为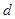 ,则
,则
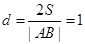 ,
,
又因为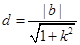 ,
,
所以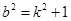 ,代入②式并整理,得
,代入②式并整理,得
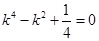 ,
,
解得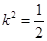 ,
,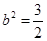 ,代入①式检验,
,代入①式检验,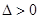 ,
,
故直线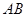 的方程是
的方程是
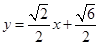 或
或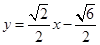 或
或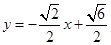 ,或
,或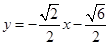 .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目

 如图,
如图,

 中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点
中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点