题目内容
若实数t满足f(t)＝－t，则称t是函数f(x)的一个次不动点．设函数
与反函数的所有次不动点之和为m，则m＝______
0
解析试题分析：函数y=lnx的图象与直线y=-x有唯一公共点（t，-t）则有t=-ln（-t），ex=-x?x=ln（-x）?x=-t．故两个函数的所有次不动点之和m=t+（-t）=0．解：函数y=lnx的图象与直线y=-x有唯一公共点（t，-t）则有t=-ln（-t），而ex=-x?x=ln（-x）?x=-t．故两个函数的所有次不动点之和m=t+（-t）=0，故答案为 0．
考点：函数零点
点评：本题以新定义为载体，考查了函数图象的对称性的灵活运用，属于中档题．
练习册系列答案
相关题目
是定义在
上的增函数，其中
且
，已知
，则对于
有以下四个说法：
；②是偶函数；③最小值是0；④在定义域内单调递增.
的定义域为
，若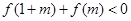
，则实数m的范围是_______.
为区间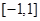
上的奇函数，则它在这一区间上的最大值是 .
的解所在区间为
，则
= ．
为偶函数，则m=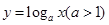 
的定义域和值域均为
,则
的范围是____________。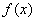
是R上的奇函数
.
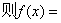，则
______________。