题目内容
已知双曲线的标准方程为 ,F为其右焦点,A1,A2是实轴的两端点,设P为双曲线上不同于A1,A2的任意一点,直线A1P,A2P与直线x=a分别交于两点M,N,若
,F为其右焦点,A1,A2是实轴的两端点,设P为双曲线上不同于A1,A2的任意一点,直线A1P,A2P与直线x=a分别交于两点M,N,若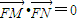 ,则a的值为( )
,则a的值为( )A.

B.
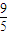
C.

D.

【答案】分析:双曲线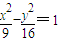 ,右焦点F(5.0),A1(-3,0),A2(3,0),设P(x,y),M(a,m),N(a,n),由P,A1,M三点共线,知
,右焦点F(5.0),A1(-3,0),A2(3,0),设P(x,y),M(a,m),N(a,n),由P,A1,M三点共线,知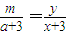 ,故m=
,故m=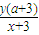 ,由P,A2,N三点共线,知
,由P,A2,N三点共线,知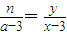 ,故n=
,故n=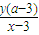 ,由
,由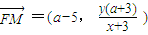 ,
,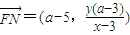 和
和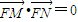 ,能求出a的值.
,能求出a的值.
解答:解:∵双曲线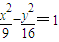 ,右焦点F(5,0),A1(-3,0),A2(3,0),
,右焦点F(5,0),A1(-3,0),A2(3,0),
设P(x,y),M(a,m),N(a,n),
∵P,A1,M三点共线
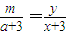 ,
,
∴m=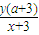 ,
,
∵P,A2,N三点共线,
∴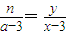 ,
,
∴n=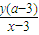 ,
,
∵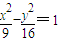 ,
,
∴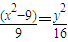 ,
,
∴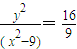 ,
,
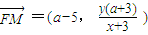 ,
,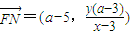 ,
,
∴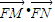 =(a-5)2+
=(a-5)2+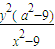 =(a-5)2+
=(a-5)2+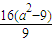 ,
,
∵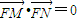 ,
,
∴(a-5)2+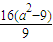 =0,
=0,
∴25a2-90a+81=0,
∴a=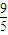 .
.
故选B.
点评:本题考查双曲线的性质和应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.解题时要认真审题,注意向量知识的合理运用.
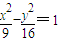 ,右焦点F(5.0),A1(-3,0),A2(3,0),设P(x,y),M(a,m),N(a,n),由P,A1,M三点共线,知
,右焦点F(5.0),A1(-3,0),A2(3,0),设P(x,y),M(a,m),N(a,n),由P,A1,M三点共线,知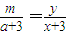 ,故m=
,故m=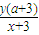 ,由P,A2,N三点共线,知
,由P,A2,N三点共线,知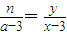 ,故n=
,故n=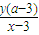 ,由
,由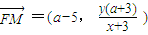 ,
,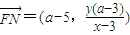 和
和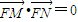 ,能求出a的值.
,能求出a的值.解答:解:∵双曲线
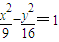 ,右焦点F(5,0),A1(-3,0),A2(3,0),
,右焦点F(5,0),A1(-3,0),A2(3,0),设P(x,y),M(a,m),N(a,n),
∵P,A1,M三点共线
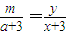 ,
,∴m=
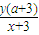 ,
,∵P,A2,N三点共线,
∴
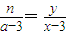 ,
,∴n=
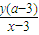 ,
,∵
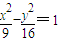 ,
,∴
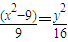 ,
,∴
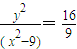 ,
,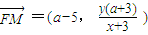 ,
,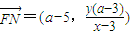 ,
,∴
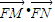 =(a-5)2+
=(a-5)2+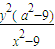 =(a-5)2+
=(a-5)2+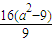 ,
,∵
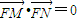 ,
,∴(a-5)2+
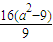 =0,
=0,∴25a2-90a+81=0,
∴a=
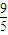 .
.故选B.
点评:本题考查双曲线的性质和应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.解题时要认真审题,注意向量知识的合理运用.

练习册系列答案
相关题目
已知双曲线的标准方程为
-y2=1,则它的焦点坐标是( )
| x2 |
| 2 |
A、(
| ||||
| B、(1,0),(-1,0) | ||||
C、(0,
| ||||
| D、(0,1),(0,-1) |
 ,F为其右焦点,A1,A2是实轴的两端点,设P为双曲线上不同于A1,A2的任意一点,直线A1P,A2P与直线x=a分别交于两点M,N,若
,F为其右焦点,A1,A2是实轴的两端点,设P为双曲线上不同于A1,A2的任意一点,直线A1P,A2P与直线x=a分别交于两点M,N,若 ,则a的值为( )
,则a的值为( )



 ,F为其右焦点,A1,A2是实轴的两端点,设P为双曲线上不同于A1,A2的任意一点,直线A1P,A2P与直线x=a分别交于两点M,N,若
,F为其右焦点,A1,A2是实轴的两端点,设P为双曲线上不同于A1,A2的任意一点,直线A1P,A2P与直线x=a分别交于两点M,N,若 ,则a的值为( )
,则a的值为( )



 ,则它的焦点坐标是( )
,则它的焦点坐标是( )
