题目内容
解答须写出文字说明、证明过程和演算步骤.
若椭圆![]() 过点(-3,2),离心率为
过点(-3,2),离心率为![]() ,⊙O的圆心为原点,直径为椭圆的短轴,⊙M的方程为(x-8)2+(y-6)2=4,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
,⊙O的圆心为原点,直径为椭圆的短轴,⊙M的方程为(x-8)2+(y-6)2=4,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线PA与⊙M的另一交点为Q,当弦PQ最大时,求直线PA的直线方程;
(Ⅲ)求![]() 的最大值与最小值.
的最大值与最小值.
答案:
解析:
解析:
|
解:(Ⅰ)由题意得: 所以椭圆的方程为 (Ⅱ)由题可知当直线PA过圆M的圆心(8,6)时,弦PQ最大 因为直线PA的斜率一定存在, 设直线PA的方程为:y-6=k(x-8) 又因为PA与圆O相切,所以圆心(0,0)到直线PA的距离为 即 所以直线PA的方程为:x-3y+10=0或13x-9y-50=0 (Ⅲ)设∠AOP=α 则∠AOP=∠BOP,∠AOB=2α 则 ∵|OP|max=10+2=12,||OP|min=10-2=8 |

练习册系列答案
相关题目

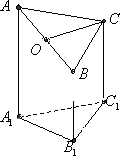

 16.(本小题满分12分)[来源:学§科§网]
16.(本小题满分12分)[来源:学§科§网] .
. 的解析式;
的解析式; ,且
,且 ,
, 的值.
的值.