题目内容
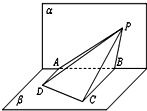如图所示，△PAB所在的平面α和四边形ABCD所在的平面β互相垂直，且AD⊥α，BC⊥α，AD=4，BC=8，AB=6．若tan∠ADP-2tan∠BCP=1，则动点P在平面α内的轨迹是（ ）| A、椭圆的一部分 | B、线段 | C、双曲线的一部分 | D、以上都不是 |
分析：由tan∠ADP=
，tan∠BCP=
，以及tan∠ADP-2tan∠BCP=1，可得|PA|-|PB|=4，根据双曲线的定义做出判断．
| |AP| |
| 4 |
| |PB| |
| 8 |
解答：解：由题意得，△ADP 和△BCP均为直角三角形，且 tan∠ADP=
=
，
tan∠BCP=
=
．
∵tan∠ADP-2tan∠BCP=1，∴|PA|-|PB|=4＜|AB|=6，故动点P在平面α内的轨迹是以A、B为
焦点的双曲线的一支，
故选C．
| |AP| |
| |AD| |
| |AP| |
| 4 |
tan∠BCP=
| |PB| |
| |BC| |
| |PB| |
| 8 |
∵tan∠ADP-2tan∠BCP=1，∴|PA|-|PB|=4＜|AB|=6，故动点P在平面α内的轨迹是以A、B为
焦点的双曲线的一支，
故选C．
点评：本题考查双曲线的定义，直角三角形中的边角关系，得到|PA|-|PB|=4＜|AB|是解题的关键．
练习册系列答案
相关题目
16、如图所示，P为△ABC所在平面外一点，PA⊥平面ABC，∠ABC=90°，AE⊥PB于E，AF⊥PC于F．求证：（1）BC⊥平面PAB；
7、如图所示，AB是圆O的直径，C是异于A，B两点的圆周上的任意一点，PA垂直于圆O所在的平面，则△PAB，△PAC，△ABC，△PBC中，直角三角形的个数是（ ）
14、如图所示，AB是圆O的直径，C是异于A，B两点的圆周上的任意一点，PA垂直于圆O所在的平面，则△PAB，△PAC，△ABC，△PBC中，直角三角形的个数是