题目内容
8.若P(x,y)∈$\left\{\begin{array}{l}{0≤x≤3}\\{0≤y≤4}\\{4x+3y-12≤0}\end{array}\right.$,则事件P(x,y)∈{(x,y)|(x-1)2+(y-1)2≤1}的概率是( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{12}$ | C. | $\frac{1}{2}$ | D. | $\frac{π}{4}$ |
分析 $\left\{\begin{array}{l}{0≤x≤3}\\{0≤y≤4}\\{4x+3y-12≤0}\end{array}\right.$表示直角三角形,{(x,y)|(x-1)2+(y-1)2≤1},表示以(1,1)为圆心,1为半径的圆面,求出相应的面积,即可求出概率.
解答  解:$\left\{\begin{array}{l}{0≤x≤3}\\{0≤y≤4}\\{4x+3y-12≤0}\end{array}\right.$表示直角三角形,其面积为$\frac{1}{2}×3×4$=6,
解:$\left\{\begin{array}{l}{0≤x≤3}\\{0≤y≤4}\\{4x+3y-12≤0}\end{array}\right.$表示直角三角形,其面积为$\frac{1}{2}×3×4$=6,
{(x,y)|(x-1)2+(y-1)2≤1},表示以(1,1)为圆心,1为半径的圆面,其面积为π,
所以所求概率为$\frac{π}{6}$,
故选:A.
点评 本题考查概率的计算,考查面积的求解,正确求出面积是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.($\frac{1}{2}$x-2y)5的展开式中x2y3的系数是( )
| A. | 5 | B. | -5 | C. | 20 | D. | -20 |
13.当m=6,n=3时,执行如图所示的程序框图,输出的S值为( )


| A. | 6 | B. | 30 | C. | 120 | D. | 360 |
17.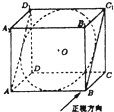 如图,长方体ABCD-A1B1C1D1中,AB=2,AD=AA1=$\sqrt{2}$.设长方体的截面四边形ABC1D1的内切圆为O,圆O的正视图是椭圆O',则椭圆O'的离心率等于( )
如图,长方体ABCD-A1B1C1D1中,AB=2,AD=AA1=$\sqrt{2}$.设长方体的截面四边形ABC1D1的内切圆为O,圆O的正视图是椭圆O',则椭圆O'的离心率等于( )
 如图,长方体ABCD-A1B1C1D1中,AB=2,AD=AA1=$\sqrt{2}$.设长方体的截面四边形ABC1D1的内切圆为O,圆O的正视图是椭圆O',则椭圆O'的离心率等于( )
如图,长方体ABCD-A1B1C1D1中,AB=2,AD=AA1=$\sqrt{2}$.设长方体的截面四边形ABC1D1的内切圆为O,圆O的正视图是椭圆O',则椭圆O'的离心率等于( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
8.阅读如图所示的程序框图,运行相应的程序,输出的结果是( )


| A. | 3 | B. | 9 | C. | 27 | D. | 81 |
 如图,已知Rt△ABC中,点O为斜边BC的中点,且AB=8,AC=6,点E为边AC上一点,且$\overrightarrow{AE}=λ\overrightarrow{AC}$,若$\overrightarrow{AO}•\overrightarrow{BE}=-20$,则λ=$\frac{2}{3}$.
如图,已知Rt△ABC中,点O为斜边BC的中点,且AB=8,AC=6,点E为边AC上一点,且$\overrightarrow{AE}=λ\overrightarrow{AC}$,若$\overrightarrow{AO}•\overrightarrow{BE}=-20$,则λ=$\frac{2}{3}$.