题目内容
已知数列{an}中,a0=0且an=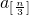 +n-3×[
+n-3×[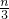 ](n∈N)(其中[x]表示实数x的整数部分),则a72的值为
](n∈N)(其中[x]表示实数x的整数部分),则a72的值为
- A.2
- B.3
- C.4
- D.5
C
分析:通过an=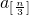 +n-3×[
+n-3×[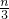 ]依次求得a0、a1、a2、a3、a4、a5、a6,找到规律后即可求得结果.
]依次求得a0、a1、a2、a3、a4、a5、a6,找到规律后即可求得结果.
解答:由题意知
a0=0=a0+0
a1=a0+1-0=a0+1
a2=a0+2-0=a0+2
a3=a1+3-3a1=a1+0
a4=a1+4-3a1=a1+1
a5=a1+5-3a1=a1+2
a6=a2+6-3a2=a2+0
依此类推得a72=a14+0=a4+2=a1+1+2=4
点评:本题考查了数列的递推式,通过递推式寻找规律是解题的关键,属于中档题.
分析:通过an=
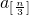 +n-3×[
+n-3×[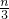 ]依次求得a0、a1、a2、a3、a4、a5、a6,找到规律后即可求得结果.
]依次求得a0、a1、a2、a3、a4、a5、a6,找到规律后即可求得结果.解答:由题意知
a0=0=a0+0
a1=a0+1-0=a0+1
a2=a0+2-0=a0+2
a3=a1+3-3a1=a1+0
a4=a1+4-3a1=a1+1
a5=a1+5-3a1=a1+2
a6=a2+6-3a2=a2+0
依此类推得a72=a14+0=a4+2=a1+1+2=4
点评:本题考查了数列的递推式,通过递推式寻找规律是解题的关键,属于中档题.

练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|