题目内容
点P(x,y)是曲线y=3lnx+x+k(k∈R)图象上一个定点,过点P的切线方程为4x-y-1=0,则实数k的值为( )A.2
B.-2
C.-1
D.-4
【答案】分析:求出曲线的导函数,把x=x代入即可得到切线的斜率,然后根据过点P的切线方程为4x-y-1=0得出切线的斜率从而求出切点的坐标,最后将切点的坐标代入曲线方程即可求出实数k的值.
解答:解:由函数y=3lnx+x+k知y′=3×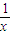 +1=
+1=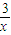 +1,
+1,
把x=x代入y′得到切线的斜率k=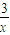 +1,
+1,
因切线方程为:4x-y-1=0,∴k=4,
∴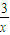 +1=4,得x=1,
+1=4,得x=1,
把x=1代入切线方程得切点坐标为(1,3),
再将切点坐标(1,3)代入曲线y=3lnx+x+k,得3=3ln1+1+k,
∴k=2.
故选A.
点评:本题主要考查学生根据曲线的导函数求切线的斜率,利用切点和斜率写出切线的方程.属于中档题.
解答:解:由函数y=3lnx+x+k知y′=3×
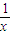 +1=
+1=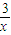 +1,
+1,把x=x代入y′得到切线的斜率k=
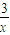 +1,
+1,因切线方程为:4x-y-1=0,∴k=4,
∴
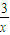 +1=4,得x=1,
+1=4,得x=1,把x=1代入切线方程得切点坐标为(1,3),
再将切点坐标(1,3)代入曲线y=3lnx+x+k,得3=3ln1+1+k,
∴k=2.
故选A.
点评:本题主要考查学生根据曲线的导函数求切线的斜率,利用切点和斜率写出切线的方程.属于中档题.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目