题目内容
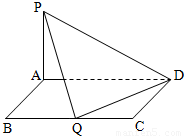
 (理科做)如图所示已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD且PA=1.建立适当的空间坐标系,利用空间向量求解下列问题:
(理科做)如图所示已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD且PA=1.建立适当的空间坐标系,利用空间向量求解下列问题:(1)求点P、B、D的坐标;
(2)当实数a在什么范围内取值时,BC边上存在点Q,使得PQ⊥QD;
(3)当BC边上有且仅有一个Q点,使得时PQ⊥QD,求二面角Q-PD-A的余弦值.
分析:(1)先建立空间直角坐标系,因为题目中有矩形ABCD,以及和这个矩形面垂直的直线,所以x,y,z轴很容易找到,再在所建坐标系中求出点P、B、D的坐标即可.
(2)要想使得PQ⊥QD,则只需
•
=0,可先求向量
,
的坐标,再计算
•
,看结果是否为0即可.
(3)要求二面角Q-PD-A的余弦值,只需求两个平面的法向量的夹角的余弦值即可,可先分别求两个平面的法向量,再利用向量夹角公式求余弦值.
(2)要想使得PQ⊥QD,则只需
| PQ |
| DQ |
| PQ |
| DQ |
| PQ |
| DQ |
(3)要求二面角Q-PD-A的余弦值,只需求两个平面的法向量的夹角的余弦值即可,可先分别求两个平面的法向量,再利用向量夹角公式求余弦值.
解答: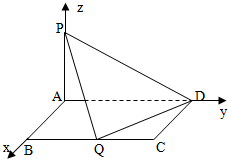 解:(1)∵PA⊥平面ABCD且ABCD为矩形,∴分别以AB,AD,AP为x,y,z轴建立如图所示的空间直角坐标系O-xyz
解:(1)∵PA⊥平面ABCD且ABCD为矩形,∴分别以AB,AD,AP为x,y,z轴建立如图所示的空间直角坐标系O-xyz
∵AP=AB=1,BC=2∴P(0,0,1),B(1,0,0),D(0,a,0)
(2)设Q(1,y,0),则
=(1,y,-1)
=(1,y-a,0)∵PQ⊥QD∴
•
=0∴1+y(y-a)+0=0即y2-ay+1=0 (*)
∵Q在边BC上,
∴a>0且△=a2-4≥0
∴a≥2,即a的取值范围是[2,+∞)
(3)当BC边上有且仅有一个Q点,方程(*)有等根,
∴y=1,此时a=2
显然平面PAD的一个法向量为
=(1,0,0)
设平面PQD的一个法向量为
=(x,y,z),则
•
=0且
•
=0
由(2)知
=(1,1,-1),
=(1,-1,0)∴
,
不妨取x=1,则y=1,z=2,
∴
=(1,1,2)
由图可知,二面角Q-PD-A为锐角,设为α
cosα=
=
=
,即二面角Q-PD-A即的余弦值为
 解:(1)∵PA⊥平面ABCD且ABCD为矩形,∴分别以AB,AD,AP为x,y,z轴建立如图所示的空间直角坐标系O-xyz
解:(1)∵PA⊥平面ABCD且ABCD为矩形,∴分别以AB,AD,AP为x,y,z轴建立如图所示的空间直角坐标系O-xyz∵AP=AB=1,BC=2∴P(0,0,1),B(1,0,0),D(0,a,0)
(2)设Q(1,y,0),则
| PQ |
| DQ |
| PQ |
| DQ |
∵Q在边BC上,
∴a>0且△=a2-4≥0
∴a≥2,即a的取值范围是[2,+∞)
(3)当BC边上有且仅有一个Q点,方程(*)有等根,
∴y=1,此时a=2
显然平面PAD的一个法向量为
| m |
设平面PQD的一个法向量为
| n |
| n |
| DQ |
| n |
| PQ |
由(2)知
| PQ |
| DQ |
|
不妨取x=1,则y=1,z=2,
∴
| n |
由图可知,二面角Q-PD-A为锐角,设为α
cosα=
|
| ||||
|
|
| 1 | ||
|
| ||
| 6 |
| ||
| 6 |
点评:本题考查了利用空间向量解决立体几何问题,属于空间向量的应用.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
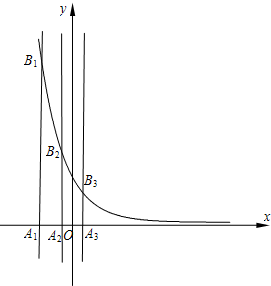 (2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数
(2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数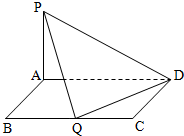 (理科做)如图所示已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD且PA=1.建立适当的空间坐标系,利用空间向量求解下列问题:
(理科做)如图所示已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD且PA=1.建立适当的空间坐标系,利用空间向量求解下列问题: